R-25. 로지스틱 회귀분석

ex) 소득이 주택보유에 미치는 영향은?

회귀분석은, 독립변수와 종속변수가 연속형 양적 데이터로 이뤄진 경우 사용

영향, 예측 계산에 사용

 

범주형 자료를 그대로 선형회귀분석을 하게 되면, 하나의 직선으로 파악하는 것이 힘들다.

범주형 자료를 변환해 비율로 나타내면 경향이 나타나게 된다. 이게 로지스틱 곡선.

 

우선 오즈로의 변환을 수행한다.

일반적 비율 = 발생확률/전체 = p/1

odds = p/(1-p) 

소득구간	명수	소유자	미소유자	소유비율	오즈
100만원 미만	100	10	90	0.10	0.111
20만원 미만	100	18	82	0.18	0.219

이런 계산을 통해, 종속변수 범위가 실수 전체구간으로 확대되어, 회귀모델로써 추정하는 게 가능

Odds비에 log를 취하여 자료를 변환한다.

 

즉, B(회귀계수)를 Exp(B)하여 odds를 얻는데, 이를 log 선형변환으로 B를 획득

위의 예에서, 호감도가 1 증가할 때 제품 구매할 확률 14.2% 증가한단 뜻

 

우도비 검정- 원값에 로그를 취하고 -2를 곱해, -2LL(log likelihood) 차이로 검정통계량 계산

이는 0에 가까울 수록 좋은 모델을 뜻

 

유사(pow(R,2)) 

---

로지스틱 회귀 · ratsgo's blog

로지스틱 회귀 · ratsgo's blog

로지스틱회귀(Logistic Regression) 쉽게 이해하기 - 아무튼 워라밸 (hleecaster.com)

로지스틱회귀(Logistic Regression) 쉽게 이해하기 - 아무튼 워라밸

Logistic Regression(로지스틱 회귀) 개념 정리 (eunsukim.me)

Logistic Regression(로지스틱 회귀) 개념 정리

 

일반적인 선형회귀 : X라는 고정변수가 있을 때, Y값이 얼마나 변하는지 그 평균을 구하는 것. 

예를 들어 나이와 혈압이 있음. 나이가 고정되어있을 때, 혈압은 얼마나 변할까?

 

그렇다면 이 연속형 숫자인 혈압 대신 범주형 변수를 이용해 회귀모델을 구축한다면 어떨까?

가령 나이에따른 암 발병 여부를 본다고 하자. 1이면 발병, 0이면 미발병이다. 그렇다면 아래와 같이 표기된다.

이러한 상황을 피하기 위해 만들어진 것이 곧 로지스틱 함수, 또는 시그모이드 함수.

로지스틱 함수는 x값으로 어떤 값이든 받지만, 무조건 0~1 사이가 출력된다. 

그림1. sigmoid

이 프로세스를 간단히 설명하면, 아래와 같다.

1. 모든 feature의 계수(coefficient)와 절편(intercept)를 0으로 초기화
2. 각 feature의 값에 계수를 곱해, log-odds를 구한다.
3. log-odds를 sigmoid 함수에 넣어서 [0,1] 범위의 확률을 구한다.
4. 계산한 확률값과 실제 Lable을 비교하여 Loss를 계산하고, 경사하강으로 최적화된 계수와 절편을 구한다.
5. 최적화된 파라미터를 구했다면, classfication threshold를 조절하여 Positive class와 Negative Class를 어떻게 나눌지 설정한다.

이 때 odds = 사건이 발생할 확률 / 사건이 발생하지 않을 확률

우선 log-odds에 대해 알아보자. 선형회귀에서는 각 feature의 값에 계수를 곱하고, 절편을 더해서 예측값을 구했다.

y=β0+β1x1+β2x2+...+βpxp+ε    #예시

이 값의 범위는 -∞에서 + ∞까지다. 로지스틱 역시 마찬가지인데, 여기에서 예측값 대신 log-odds를 구하는 차이가 있다.

예를 들어 시험에 합격할 확률이 0.7이라면, odds = 0.7/0.3 = 2.33

그리고 여기에 로그를 취한 log(2.33) = 0.847이 곧 log-odds가 된다.

 

왜 이런 짓을 하는가? 이를 통해, 숫자가 ∞로 발산하는 걸 어느정도 제어가 가능하다(단 -∞로는 아직 제어가 불가).

 

그러나 실제 계산상황에서는 여러 feature에 계수를 곱하고 절편을 더해야 하기에, 위의 '시험합격확률'처럼 하기에는 어렵다. 따라서 dot-product를 통해 log-odds를 구한다.

아래의 예제를 생각해보자. 두 개의 feature가 있고, 임의로 설정된 계수가 있다.

log_odds = np.dot(features, coefficients) + intercept

이런 방식을 통해 각 학생 3명의 log-odds를 구했다.

 

아까 말했다시피, sigmoid에 넣는다고 했다. 이는 -∞에서 + ∞까지의 값을 어느 정도 제어하기 위함이다. 이것이 곧 3과정.

#sigmoid
1/ (1+np.exp(-z))

이제 4과정이다. 로스를 구해서, 계수와 절편을 적절한 값으로 만들어야 한다. 로지스틱회귀함수의 Loss계산은 아래다.

m : 총 데이터 수 / y_i : 데이터샘플 i의 분류 / z_i : 데이터샘플 i의 log-odd / h(z_i) : 데이터샘플 i의 log-odd의 sigmoid, 즉 데이터샘플 i가 분류에 속할 확률

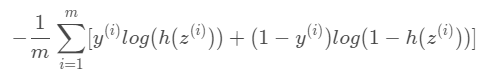
Forward-Forward의 loss함수와 매우 비슷하게 생겼다.

g_pos = self.forward(x_pos).pow(2).mean(1)
g_neg = self.forward(x_neg).pow(2).mean(1)
            
# The following loss pushes pos (neg) samples to
# values larger (smaller) than the self.threshold.
loss = torch.log(1 + torch.exp(torch.cat([
                -g_pos + self.threshold,
                g_neg - self.threshold]))).mean()

또는 Forward-Forward의 Positive 확률이랑도 비슷하게 생김.

이 때 각 파라미터는 아래와 같다.

• m:데이터 총 개수
• y_i: 데이터 샘플 i의 분류
• z_i: 데이터 샘플 i의 log-odd
• h(z_i): 데이터 샘플 i의 log-odd의 sigmoid (즉, 데이터 샘플 i가 분류에 속할 확률)

왜 h(z_i)가 데이터샘플 i가 분류에 속할 확률인지는 간단한 예를 통해 볼 수 있다.
만약 50%확률 합격, 50%확률 탈락이라 하자. 그러면 0.5/0.5=1에서 log(1)=0이다.
또한 sigmoid(0)=0.5다. 따라서, 하나의 데이터샘플 i에 대해 log-odd및 sigmoid를 구하면, 해당 샘플이 '시험에 합격하는 영역 내에 있을 확률'을 구할 수 있다.

위의 보라색으로 칠한 부분을 보자. 실제로 sigmoid(0.847)=0.699...=0.7이다.

 

만약 y=1=학생이 시험에 합격한 경우, 손실은 아래와 같다.

반면 y=0=학생이 시험에 탈락한 경우, 손실은 아래와 같다.

그냥 학생이 시험에 통과할 확률에 로그/아닌 확률에 로그를 씌웠다. 이를 그래프로 나타내면

위와 같다. 

이제는 경사하강법을 이용해, loss를 최소화시키는 계수와 절편을 찾으면 됨.