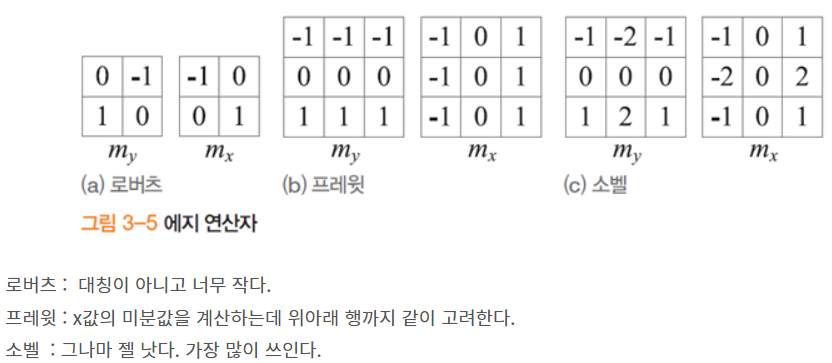
비전 3) 에지 검출

버츄얼유튜버

비전 3) 에지 검출

두원공대88학번뚜뚜 2021. 12. 15. 12:25

에지 : 물체의 경계를 표현하나, 거짓 부정이나 거짓 긍정(엣지 실종, 거짓 엣지)가 발생한다.

이 오류의 최소화 방법?

각 픽셀 사이의 명암 변화를, 도함수를 통해 구하면 갑자기 색이 확 바뀌는 구간을 찾을 수 있다.

이산공간에서 가장 작은 단위는 1이므로, 증가량을 1로 잡을 경우, 이는 (-1, 1)의 마스크로 영상 f를 컨벌루션하는 것과 같다. 이 때, 4를 임계값으로 설정하여 이진화하면, 세번째 줄과 같은 영상을 얻는다. 이 때, 1을 갖는 곳이 에지화소이며, f'(x)는 에지마스크라 부른다.

5에서 9로 바뀌는 순간, 4가 증가한다. 즉 이곳이 에지.

두 번 미분한 모델에서, 계단에지는 4 다음 -4로 바뀌는 영교차가 발생한다. 램프에지는 에지가 시작하는 위치 7에서는 -1가 나타나고, 끝나는 위치 10에서는 1이 나타나 그 사이에 영교차가 발생한다. 따라서,

1차 미분에서는 봉우리를, 2차 미분에서는 영교차를 찾으면 된다.

그러나 현실에 바로 적용하긴 무리고, 불안정한 광학으로 인해 스무딩 작업이 필요하다.

2차원 상에서는 위와 같이 확장이 가능하다. 그러나 잡음에 대처하지 못하는 약점이 있다. 따라서 마스크를 d*d 크기의 정방향으로 확장해, 연산자 자체가 스무딩 효과를 지니도록 한다.

에지 강도 및 방향

그래디언트는 벡터이기에, 에지 강도 및 방향을 알 수 있다.

에지 방향은, 그래디언트 방향에 수직이다.

위 그림에서, 경계선 상의 한 점에 마스크 mx를 적용하면 음수가 되어, dx는 왼쪽을, dy는 양수가 되어 아래를 가리킨다.

dx와 dy에 따라 그레디언트 방향이 정해지고, 이에 수직을 이루도록 에지 방향이 결정된다.

이 때, 에지 방향을 그 방향을 바라보고 설 때 왼쪽은 밝고 오른쪽은 어두운 것으로 정한다 할 때,

에지 방향은 [0, 360]의 범위를 갖는다.

영교차 이론

미분은 잡음을 증폭시키는 문제점이 있기에, 스무딩이 중요하다.

이 때, 가우시안 스무딩은 잡음에 대처하며, 에지의 세밀함 조절이 가능하다.

어두운 배경에 폭이 2, 4, 8인 물체가 놓인 영상이 있다 가정하자. 이 떄, 매개변수에 따라 에지가 검출되거나, 약해지는 것을 볼 수 있다. 이처럼, σ의 값으로 스무딩 정도(에지의 스케일)를 조절할 수 있다.

따라서, 이 매개변수를 조정해 스무딩 정도를 조절, 에지스케일을 정하거나

크게하여 큰 물체의 에지만 추출하거나, 작게 해 디테일을 살리는 등 여러 효과가 가능할 것이다.

이 때, 가우시안 함수에 대해 보자.

표준편차가 클 수록, 좌우로 넓게 퍼지며 봉우리는 낮아진다. 즉, 매개변수가 클 수록 가우시안의 영향력 범위가 넓다.

매개변수가 2일 땐, 약 x=+-6의 범위의 마스크를 만들면 매우 적절한 크기의 샘플링용 마스크가 될 것이다.

이것보다 작다면, 오차가 커서 영상품질이 떨어지고, 크다면 더 나은 정보를 기대하기 어렵다.

Marr의 에지검출 알고리즘은 이렇게 표현이 가능하다.

LOG 필터

위에서, 라플라시안 연산자란 무엇인가?

어떤 함수 f(y,x)의 라플라시안은, y와 x의 2차 편도함수를 더한 것이다.

위의 알고리즘에서, 1행에서 가우시안을 이산필터로 근사화 + 2행에서 라플라시안을 이산필터로 근사화

이를 하면, 2번에 걸치는 근사화로 오차가 커짐 + 컨벌루션도 2회 수행하기에 계산효율이 낮음.

이를 합치면 더 나을 것이다. 이것이 라플라시안 오브 가우시안, LOG이다.

위의 라플라시안 식의 각 f에 가우시안 G(y,x)를 대입하면, 다음과 같이 가우시안에 계수를 곱한 꼴이 된다.

영교차 검출

위의 알고리즘의 1행의 결과 영상을 g라 하면, g(j,i)=0인 화소 중 마주보는 이웃이 서로 다른 부호를 가졌다면, 이를 영교차 점으로 보고 b(j,i) = 1로 둘 수 있을 것이나, 실제론 잡음 등으로 이러한 품질의 기대가 힘듬

따라서, 우선

여덟개의 이웃 중 마주보는 화소 쌍 4개를 조사 하여, 두개 이상이 서로 다른 부호를 갖고

부호가 다른 쌍의 값 차이가 임계값을 넘을 때

영교차라 본다.

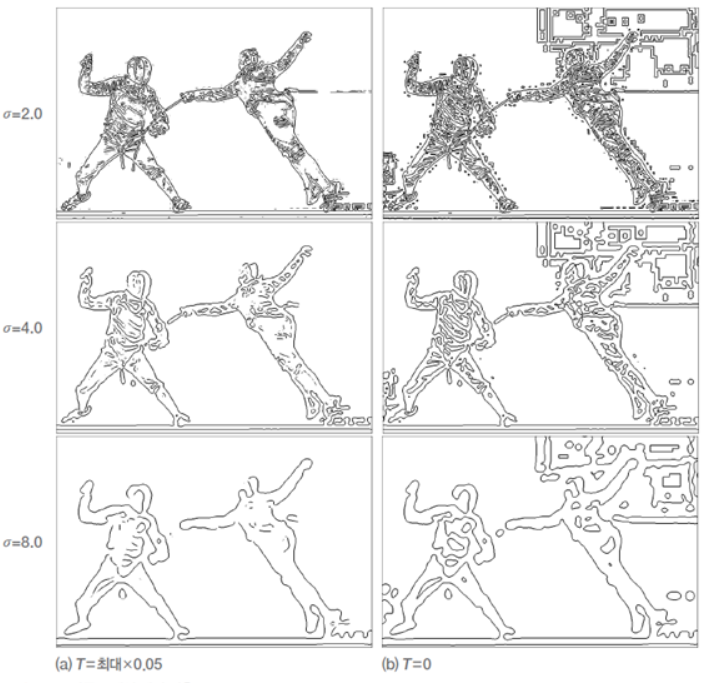
아래 그림은, 분산이 2, 4, 8인 LOG필터를 같은 영상에 적용한 결과이다.

왼쪽 열의 영상은 LOG를 적용해 얻은 영상 g의 최대값에 0.05를 곱한 값을 임계값으로, 오른쪽은 0을 임계값으로 썼다.

분산이 작을 땐, 세밀한 에지도 검출되지만, 커질수록 그렇지 않다.

캐니 에지

1) 1차원 계단 에지에 화이트 잡음이 첨가되었다 가정하고, 가우시안에 1차 미분을 적용해 최적화하면 좋다.

2) 이를 2차원으로 확장할 때, 그레디언트 방향을 알아내 미분을 수행해야 한다.

3) 결과 영상에 '소벨 연산자'를 적용해 이것을 알아내는 게 가능하나, 에지영상이 두껍단 문제가 있다.

4) 따라서, 비최대억제 & 이력임계값 단계를 적용하여 이를 해결함과 동시에 거짓긍정 문제를 해결한다.

3행의 비최대억제란, 자신의 이웃보다 크지 않은 화소를 '에지가 아닌 것'으로 결정함.

회색의 화소가 p(방향)에 대한 이웃 두 화소이고, p의 에지 강도가 두 이웃보다 크면 에지, 아니면 안됨.

이 과정에서, "실제론 에지가 아닌데 에지라 판정된" 경우도 있다. 이를 대비해, 4행에서

임계값 T를 정하고, 에지 화소 p의 에지 강도 S(p) : T이면 거짓 긍정으로 보고 제거

하는 과정을 거친다.

T가 높다면 거짓긍정은 제거를 잘할 테지만, 에지강도가 낮은 진짜 에지를 제거하는 경우가 있다(거짓부정).

T가 낮다면, 거짓긍정의 문제가 그대로 남는 경우가 있다.

두 개의 임계값 T_high와 T_low를 쓴다. 에지 추적은 T_high를 넘는 화소(=신뢰도가 높은 화소)에서 시작하며,

시작 화소가 정해지면, T_low를 넘는 화소를 대상으로 에지를 추적한다. 즉, 이웃 화소가 추적 이력이 있으면, 자신은 신뢰도가 낮더라도 에지로 간주된다.

분산이 커질수록 디테일이 사라지며, 이력 임계값이 높은 오른쪽이 에지가 적게 검출됨.

왼쪽이 low한 임계값, 오른쪽이 high한 임계값

Canny(f, img_edge, 50, 200);

컬러 에지

RGB상에서의 검출 방법은, 각 채널에서 독립적으로 한 다음 하나로 결합한다.

선분 검출

위의 알고리즘은 에지화소를 1, 비에지화소를 0으로 활용한다.

이웃한 에지화소를 연결한 '에지토막'을 만들어 응용하고, 직선으로 근사화하는 방식도 있다.

위의 알고리즘들은 두꺼운 에지를 만들기도 하는데, 이런 경우 선분으로 보기엔 어렵고, 낭비다. 1이면 되는데.

따라서, 캐니의 경우 이를 '에지 강도' 및 '에지 방향 정보'를 이용해, 다음 화소를 결정한다.

세선화

에지의 두께를 1로 변환하는 것.

마스크의 0은 비에지, 1은 에지를 뜻하고 x는 0과 1 어느 것이라도 좋다는 기호이다. 이 네 개의 마스크는 하나의 그룹을 형성하는데, 위 그림은 화소 p의 이웃 n_4가 0인 그룹이다.
더 효율적으로 계산하기 위해 네 개의 마스크 대신 논리식 s4를 검사해도 같은 결과를 얻는다. ‘는 부정, +는 or, dot은 and이다.

이 과정을 한번 적용하면 바깥쪽에서 한 화소 두께를 벗기는 셈이 되는데, 원래 SPTA는 더 이상 변화가 없을 때까지 반복하지만 보통 두께는 2~3이므로 두 번만 적용해도 충분하다.

import numpy as np
import cv2
import matplotlib.pyplot as plt
from util import *


def SPTA(img):
    '''
    n5 n6 n7
    n4 p  n0
    n3 n2 n1
    :param img:
    :return:
    '''
    img = img>0
    n4 = np.pad(img[:, :-1], ((0, 0), (1, 0)))
    n0 = np.pad(img[:, 1:], ((0, 0), (0, 1)))
    n6 = np.pad(img[:-1, :], ((1, 0), (0, 0)))
    n2 = np.pad(img[1:, :], ((0, 1), (0, 0)))
    n1 = np.pad(n2[:, 1:], ((0, 0), (0, 1)))
    n7 = np.pad(n6[:, 1:], ((0, 0), (0, 1)))
    n3 = np.pad(n2[:, :-1], ((0, 0), (1, 0)))
    n5 = np.pad(n6[:, :-1], ((0, 0), (1, 0)))
    n0_logic = np.logical_not(n0) & (n4 & (n5 + n6 + n2 + n3) & (n6 + np.logical_not(n7)) & (n2 + np.logical_not(n1)))
    n4_logic = np.logical_not(n4) & (n0 & (n1 + n2 + n6 + n7) & (n2 + np.logical_not(n3)) & (n6 + np.logical_not(n5)))
    n2_logic = np.logical_not(n2) & (n6 & (n7 + n0 + n4 + n5) & (n0 + np.logical_not(n1)) & (n4 + np.logical_not(n3)))
    n6_logic = np.logical_not(n6) & (n2 & (n3 + n4 + n0 + n1) & (n4 + np.logical_not(n5)) & (n0 + np.logical_not(n7)))
    logical = n0_logic+n4_logic+n2_logic+n6_logic

    return np.uint8(np.where(logical,False,img))*255

img = cv2.imread('C:/Users/is7se/source/repos/OpencvStudy/OpencvStudy/img/test_nanami2.png',cv2.IMREAD_GRAYSCALE)

plt.imshow(img,cmap='gray')
plt.show()

gau_img = gaussian_blur(img,1)
canny_img = canny(gau_img,30,75)


fig = plt.figure()
plt.subplot(121)
plt.imshow(img,cmap='gray')
plt.xlabel('original')

plt.subplot(122)
plt.imshow(canny_img,cmap='gray')
plt.xlabel('original')
fig.tight_layout()
plt.show()

spta_img = SPTA(canny_img)

fig = plt.figure(figsize=(13,13))
plt.subplot(121)
plt.imshow(canny_img,cmap='gray')
plt.xlabel('canny')

plt.subplot(122)
plt.imshow(spta_img,cmap='gray')
plt.xlabel('spta_img')
fig.tight_layout()
plt.show()

fig = plt.figure(figsize=(13,13))
plt.subplot(121)
plt.imshow(canny_img[250:350,200:300],cmap='gray')
plt.xlabel('canny')

plt.subplot(122)
plt.imshow(spta_img[250:350,200:300],cmap='gray')
plt.xlabel('spta_img')
fig.tight_layout()
plt.show()

이 에지의 추적 방법

허프 변환

이미지에서 모양을 찾는 방법.

이미지 내의 픽셀들 중, 서로 직선관계를 갖는 픽셀만 골라내자

lines = cv2.HoughLines(img, rho, theta, threshold, lines, srn=0, stn=0, min_theta, max_theta)

rho : 거리측정 해상도(0~1)
theta : 각도, 라디안 단위
threshold : 직선으로 판단할 최소한의 동일 개수. 작다면 정확도감소&검출수 증가, 크면 정확도증가&검출수감소
lines : 검출결과, N*1*2 배열
srn, stn : 멀티스케일 허프변환에 사용, 선 검출에선 사용 안함
min_theta, max_theta: 검출을 위해 사용할 최대(최소) 각도

원리: 이미지 내에 여러 개의 픽셀이 있다. 이 픽셀들을, 하나하나 삼각함수를 이용해

y = mx+c를 r=xcos(theta) + ysin(theta) 형식으로 변환하여 비교한다.

각 픽셀(점)을, theta를 0~180까지 변화를 주면서 원점까지의 거리를 계산한다.

그럼 위 그림의 아래 angle, dist 2차원 배열을 얻게 된다.

잘 보면 60도에서 매우 값이 유사한 것을 볼 수 있다! 즉, 세 점을 연결하는 거리 80짜리 60도의 직선의 방정식을 구했다.

절차

1) 누적배열 A를 0으로 초기화

2) 에지 점(y,x)에 대해, ycos(theta) + xsin(theta) = p를 지나는 A의 칸을 1 증가시킴.

3) 모든 에지를 처리하고, 임계값을 넘는 지역 최대점을 검출해 답으로 취함.

RANSAC

인라이어와 아웃라이어가 혼합된 샘플 집합이 주어진 상황에서, 인라이어를 찾아 모델을 적용시키는 기법

1) 임의의 두 개의 샘플 선택

2) 직선의 방정식 구함

3) 나머지 샘플에 대해 이 모델에 적합한(이 직선 상에 있는 점) 구함

4) 이 점이 인라이어, 나머지가 아웃라이어

위의 알고리즘은, 3행에서 '임의로 에지화소를 선택하는 것'을 에지 방향과 강도를 추가하는 것으로 성능 개선 가능

즉, 에지 강도가 높은 화소와 에지 방향이 비슷한 화소 쌍이 선택될 가능성 높이는 방안의 사용 가능

간단 정리

1) 에지 검출은, 영상의 명암, 컬러, 텍스처와 같은 특성이 급격히 변하는 지점 검출 작업이다.

1-1) 화면을 1차미분하고, 특정값(봉우리)을 임계값으로 설정해 이진화하면 얻게 되는 지점이 곧 에지화소이다.

1-2) 화면을 12차미분하면 영교차하는 부분이 나타난다. 즉, 1차미분에선 봉우리를, 2차미분에선 영교차를 찾으면 된다.

2) 보통의 화면이 불안정할 수 있기에, 스무딩 작업을 통해 부드럽게 해준다. 소벨 연산자는 화소의 값 변화량 분석에 많이 쓰인다.

3) 에지 강도는 화소가 에지일 가능성(confidence)를 나타낸다. 이는 gradient 방향에 수직이다. 그림(a) 참조.

4) 스무딩작업은 잡음에 대처하고, 다중스케일을 얻을 수 있는 효과가 있다. 이 때, 스무딩 작업에 있어 가우시안의 분산을 크게 하면 영상 디테일이 사라져, 큰 물체의 에지만 추출되고, 작게 하면 디테일에 해당하는 에지까지 추출이 가능하다.

5) 연산자는 소벨 연산자, 그리고 가우시안을 활용한다.

6) 캐니에지는, 아래와 같은 순서를 지닌다.

6-1) 가우시안에 1차 미분을 적용해 화면을 최적화한다.

6-2) '소벨연산자'를 이용해, 그레디언트 방향을 알아내 미분을 수행한다. 그러나 에지 영상이 두꺼울 수 있다.

6-3) 비최대억제 & 이력임계값 단계를 적용한다. 이 비최대억제 = 이웃보다 크지 않은 화소는 에지로 인정하지 않기

7) 허프변환이란, 일직선 상에 있다고 지각하는 점을 한 곳으로 모으는 일종의 에지 연결 작업이다.

7-1) 각 픽셀들을, theta를 0~180까지 변화를 주면서, 원점까지의 거리를 계산. 식은 y = mx+c를 r=xcos(theta) + ysin(theta) 형식으로 변환

7-2) 누적배열 A를 0으로 초기화 후, 에지 점(y,x)에 대해, ycos(theta) + xsin(theta) = p를 지나는 A의 칸을 1 증가시킴.

7-3) 모든 에지를 처리하고, 임계값을 넘는 지역 최대점을 검출해 답으로 취함.