비전 6) 특징기술

SIFT 기술자:

추출한 특징인 "키포인트"는 (y, x, σ)의, 위치와 스케일 정보를 담는 것으로 표현한다.

SIFT특징은, 여러 옥타브로 구성된 피라미드 구조에서 검출되며, 키포인트가 검출된 옥타브 σ와 옥타브 내의 스케일 σ0, 그 옥타브 영상에서의 위치 (r,c)가 뎜겨있다. 

 

다음으로, 회전 변환을 고려하자. 회전이 발생하면 윈도우의 방향 역시 조절되어야 하며, 따라서 SIFT는 기술자를 추출하기 이전에 지배적인 방향(dominant oreinetation)을 찾는다. 이는, 키포인트를 중심으로 일정 크기의 윈도우를 씌우고, 윈도우 내의 화소집합에 대해 그레이디언트 방향 히스토그램을 구해 알아낸다.

이 때, 10도 간격으로 방향을 양자화해, 36개 칸을 가진 히스토그램을 사용한다.

가우시안을 씌워, 그레디언트 크기를 가중치로 곱함과 동시에, 중심에서 멀어질수록 더 작은 가중치를 곱한다. 이렇게 구한 히스토그램에서 가장 큰 값을 갖는 방향을 지배적인 방향으로 삼는다.

 

이렇게 회전변환에 무관한 방향을 얻었으니, 하나의 키포인트는 위치, 스케일, 방향정보를 지닌 (y,x,σ,theta)로 표현된다.

이 지배적 방향 theta가 기준이 되도록 좌표계를 설정하며, 방향불변성이 달성되었으면 4*4개의 블록으로 나눈다.

한 블록은 자신에 속한 화소의 그레디언트를 계산한 후, 8단계로 양자화된 그레디언트 크기를 가중치로 사요앟여, 가우시안을 씌워 중심에서 멀어질수록 작은 가중치를 곱한다. 이를 통해, 4*4*8=128차원의 특징벡터 x가 추출된다.

 

광도불변성은 x를 벡터의 크기 ||x||로 나눠 단위벡터로 변환한 다음, 이 중 0.2보다 큰 요소가 있으면 0.2로 바꾸고 다시 단위벡터로 변환한다.

최종적으로, 스케일, 회전, 광도 변환에 불변한 128차원의 특징벡터 x가 만들어졌다.

 

입력영상 f는 기술자가 포함된 SIFT특징(yi, xi, σi, theta_i, xi)로 표현된다. 이 집합을 다음 단계인 매칭 과정에 입력해, 서로 다른 두 영상에서 매칭 쌍을 찾는데 쓴다.

구현방법은 Hess2010 + http://robwhess.github.io/opensift/ 에서 쓸 수 있다.

 

SIFT의 변형(개선)

PCA-SIFT

GLOH

모양 콘텍스트

SIFT포함 여러 개의 성능테스트 결과는 Mikolajczyk2005a에서 볼 수 있다.

 

이진기술자

한정된 자원(성능이 떨어지는 상황)에서 영상 이미지에서 검출을 해야 할 경우, 상당히 많은 시간이 소요된다. 이 경우,

특징점 주변의 두 개의 화소를 비교 싸응로 삼아, 명암값을 비교해 0 또는 1의 이진값을 생성

BRIEF는, 가우시안 분포로부터 두 점 발생시켜 비교쌍 생성. 따라서 스케일, 회전 변환에 대처하지 못함.

 

 

영역 기술자

5장의 영상분할을 통해 영역을 생성시킴. 여기서부터 풍부한 정보를 추출해본다.

 

모멘트 : 어떤 종류의 물리적 효과가 하나의 물리량뿐 아니라, 그 물리량의 분포상태에 따라 정해질 때 정의되는 양.

1) 모멘트 - 화소나 화소의 명암값의 통계적 분포를 측정하고, 이로부터 정보를 추출

영상 픽셀의 강도에 대한 특정 가중평균. 즉, 바이너리 이미지의 x축과 y축이 가지는 고유 특성.

각 이미지의 x축과 y축의 픽셀번호를 더한 값.

M_a,b는 a와 b를 각각의 화소의 좌표로 하는 물체의 모멘트.

이 식을 이용해, 영역 R의 면적과 중점(무게 중심)의 계산이 가능.

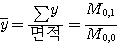
위의 y, x가 각각 영역 R의 무게중심 좌표임. 이 때 면적 = M0,0이 되는 걸 볼 수 있는데, 이는 위치불벼넝이다. 그러나 중점좌표는 그렇지 않다. 당연한 소리다. 영역 R은 어디로 옮기든 그 면적은 그대로니까! 하지만 무게중심은 위치에 따라 바뀐다. (x,y)좌표가 바뀔테니, M_a,b는 바뀌는 수밖에.

반대로, y와 x는 크기불변이고 회전불변이지만, 면적은 그렇지 않다. 

위의 중점을 원점으로 간주하고 계산한 모멘트

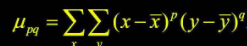
이 중심모멘트를 통해, 화소가 열/행/열, 행 모두에 대해 얼마나 넓게 퍼져있는지 측정이 가능하다.

열분산 vcc = m_2,0/a(면적)
행분산 vrr = m_0,2/a
혼합분산 vrc = m_1,1/a

그 외 명암영역의 모멘트와 그 중점, 중심모멘트도 존재.

 

모양

한 화소를 폭, 높이가 1인 네모로 간주할 때, 

n_even = 짝수체인 개수

n_odd = 홀수체인 개수

둘레 p = n_even + n_odd * sqrt(2)

둥근 정도 r = 4pi*면적/pow(r,2)

길쭉한 정도 e = 면적/pow(w,2), 이때 w= 두께

주축방향 theta = 1/2*arctan(2m_1,1/(m_2,0 - m_0,2))

 

푸리에 기술자

- 이산 푸리에 변환으로 입력된 이산신호 s(.)로부터 계수 t(.)를 구하는 식 : 구글링

이 때, t(u)가 정의된 u축은 주파수 도메인

 

입력 이산신호 s(i) = yi + jxi

영역 R을 t(u) = 1/sqrt(n) * s(i) * exp(-j*2*pi*u*i/n)의 형태로 변환한 다음,

위의 입력 이산신호를 이용해 푸리에 변환을 구한다.

다음으로, x=(real(t(0)), img(t(0)), .... real(t(d-1)), imag(t(d-1))) 의 x가 곧 푸리에 기술자가 됨.

 

텍스처(를 이용한 영상분할은 Jain90, Arbelaez2011)

풀과 깃털은 에지가 밀집도, 방향에서 다른 양상을 보인다. 이렇게, 에지는 텍스처를 나타내는 좋은 정보 중 하나다.

T_edge = (busy, mag(i), dir(j__, 0<=i<=q-1, 0<=j<=7
이 때 busy = 영역 에지 화소 수/영역 화소 수
mag(i) = 에지 화소의 에지 강도를 q단계로 양자화해서 구한 히스토그램
dir(i) = 8방향으로 양자화된 에지 방향 히스토그램

텍스처를 나타내는 또다른 방법 : 영역 구성하는 화소의 명암 히스토그램을 이용하는 것. 정규명암 히스토그램 hat_h(l), l이 0, 1, .... L-1 이라 하자. 이 때, 아래 식은 히스토그램의 r차 모멘트이다.

mu_r = sigma(from l=0 to L-1) { (l-m)^r * hat_h(l) }
이 때 m = sigma(from l=0 to L-1) { l * hat_h(l) }

텍스처 기술자는 아래와 같다. smooth와 skew는 바로 위의 식을 통해 알 수 있으며, 각각 영역의 부드러운 정도 & 히스토그램이 밝은 쪽, 어두운 쪽 중 어디에 치우쳤는지 알려줌. uniform은 영역이 얼마나 균일한지 측정, entropy는 변화가 얼마나 심한지 알려줌.

T_histogram = (smooth, skew, uniform, entropy)

smooth = 1 - 1/(1+m2/(L-1)^2))
skew = m3
uniform = sigma(from l=0 to L-1) hat_h(l) ^2
entropy = -sigma(from l=0 to L-1) hat_h(l) * log2_hat_h(l)

근데 이건 명암히스토그램을 사용하기에, 서로 다른 세 텍스처는 구분 못한다.

 

지역관계 기술자를 통해 풀 수 있다.

동시발생행렬

hat_o_j,i = o_j,i / n = 동시발생행렬 O의 (j,i)에 있는 요소

이 O로부터 균일성, 엔트로피, 대비(contrast), 동질성, 공관계의 특징 추출이 가능한데, 모든 화소가 같은 값을 갖는 완벽한 균일 영상일 때 1이 된다.

 

지역이진 패턴은 두번째 텍스처 기술자. 

현재 회색으로 표현된 부분을 조사중. 여기에 3*3 윈도우를 씌우고, 현 화소값인 150과 여덟개 이웃을 비교하여, 크면 1, 작으면 0으로 채운다. 그런 후 8비트 이진수로 변환한 다음, 10진수로 얻으면 50이 획득된다.

이렇게 모든 화소에 대해 해당 작업을 처리해서 각각 0~255를 획득하고 나면, 지역이진패턴(LBP)라 하는, 이들 정수 히스토그램을 얻을 수 있다.

Mat image = imread(이미지);
Mat gray;
cvtColor(image, gray, CV_BGR2GRAY);
Mat lbp(image.size(), CV_8U, Scalar(0)));

for(int i=1; i<gray.lows; i++) {
	for(int j=1; j<gray.cols - 1; j++) {
    	uchar t[9];
        for(int k=0; k<3; k++) {
        	for(int l=0; l<3; l++) {
            	t[k*3+l] = gray.at<uchar>(i+k-1, j+l-1);
            }
        }
        uchar currVal = ReturnDecimalVal(t);
        
        lbp.at<uchar>(i,j) = currVal;
    }
}

uchar ReturnDecimalVal(uchar *t){
	uchar val=0;
    uchar center = t[1*3+1];
    bool chk[9];
    int calStance[8] = {3,6,7,8,5,2,1,0}; //계산순서는 임의로 설정해도 됨.
    
    for(int k=0; k<3; k++) {
    	for(int l=0; l<3; l++) {
        	chk[k*3+l] = center >= t[k*3+l] ? true : false;
        }
    }
    
    for(int i=7; i>=0; i--) {
    	val += chk[calStance[7-i]] * pow(2, i);
    
    return val;
}

LBP는 명암이 균일한 곳에서는 불안정하다. 즉, 위의 조사하는 부근의 명암값이 150로 균일할 때, 실제론 작은 오차가 섞인 150+-2 같은 명암이 주위에 임의로 분포를 띨 것이다.

 

LTP는 이 단점을 개선했다. (in Ojala2002, Ojala96, Howarth2004)

현 화소값이 150이고, t(매개변수)가 5로 설정되어 있는 경우, 이웃이 145보다 작으면 -1, 155보다 크면 1로 설정한다. 그 이외의 경우엔 0을 넣는다. 이 경우, -1 -1 0 1 -1 0 1 -1이 만들어지는데, 이는 두 개의 이진코드열 00010010, 11001001 로 변환이 된다. 256개의 칸을 가진 히스토그램 두 개가 생성된, 512차원의 특징벡터가 만들어졌다.

 

LBP는 무언갈 인식하는데 활용된다. 이웃화소간의 상대적 명암 크기를 사용하기에, 조명전환에 불변인 특성을 지녔다.

단, 크기변환엔 적절히 대응하지 못한다. 즉, 사람검출에 HoG와 더불어 잘 쓰인다.

 

https://d-in-cloud.tistory.com/29?category=795114 

[LIBSVM]LBP와 SVM(머신러닝)을 이용한 특징점 검출

 

주성분 변환

화소가 600*450으 이미지는, 270000차원의 특징벡터를 만든다. 이는 주성분 분석으로, 정보손실을 최소화하며 차원을 줄인다. 이 방법을 아라보자.

 

우선, 학습집합 X = {x1, x2, ... xn}을 이용해, 특징 추출에 사용할 변환행렬 U를 추정해야 한다. U를 추출하고 벌어지는 특징 추출 단계는 y^T = Ux^T가 된다. 입력벡터 x와 출력벡터 y가 각각 D와 d차원이라면, U는 d*D차원 행렬일 것이다.

이렇듯 PCA의 목표는 x를 더 낮은 차원의 벡터 y로 만드는것.

https://excelsior-cjh.tistory.com/167

차원 축소 - PCA, 주성분분석 (1)

 

 

얼굴인식(고유얼굴)

with Sirovich87, Zhang97

1) 얼굴db를 통해, 평균얼굴을 만든다.

f_av(얼굴평균) = 1/n*sigma(from i-1 to n) {fi(얼굴)}

얼굴 영상은 서로 다르지만, 일정범위 안에서만 변화를 겪기에, 점이 공간에 모이고, 평균 얼굴은 이들의 중간지점에 속하게 된다.

이제 얼굴영상 fi를 PCA 입력으로 취할 수 있도록 '벡터'로 변환한다.

xi=(fi(0,0),fi(0,1),....,fi(0,N-1), fi(1,0), fi(1,1),...... fi(M-1, N-1))

벡터 xi는 D-MN차원 공간 위의 한 점으로 간주할 수 있기에, pca를 적용한다.

학습집합 X=[x1, ... xn]으로부터 평균벡터hat_x를 구하고, 각 벡터에서 평균벡터를 빼서 원점을 중심으로 분포하도록 한다.

다음으로 공분한행렬 sigma를 구하고, 이 행렬의 고유벡터와 고유값을 계산한다. 이 떄, sigma가 MN*MN이므로, MN개의 고유벡터가 얻어진다.

차원의 축소를 위해, MN개의 고유벡터 중 가장 고유값이 큰 d개만 선택한다.

선택된 고유벡터를 고유값이 큰 순서에 따라 u1, u2,... ud라 표기하고, 순서대로 U행렬의 행에 배치한다.

고유벡터 ui는 MN차원으로서의 영상의 크기와 같다. 따라서, 위의 xi식을 역으로 적용해 ui를 영상형태로 바꿀 수 있다.

고유벡터는 얼굴 형태를 띠게 되며, 고유값이 클수록 얼굴이 형태가 뚜렷하다. 이것이 고유얼굴이다.

 

---