[확통] 2
Linear regression


저 동그라미친 부분이 expectation. 이 때,


위의 식은 residual sum of squares.
식으로 표현시,

111 과 x1x2x3이 구성하는 평면에 y1y2y3이 있을 순 없다고 봐도 됨.
람다0 * (111) + 람다1 * (x1x2x3)은, 세 점이 만드는 평면 안에 있지만 y1y2y3은 아님.
projection을 할 때(보통 수직이 될 때), 나오는 람다0 람다1이 w0w1의 *임.



x가 full rank가 되려면, 위의 111 x1x2x3이 서로다른 벡터면 full rank. 두 벡터가 겹치지 않으면, 두 벡터가 2차원공간을 만듦. 그럼 이 행렬x는 full rank 2가 됨. 2차원 space를 정의하기에.
만약 1 1 1, 1.1 1.1 1.1이면 1차원이 되버림. linear independent하지 않음. basis를 형성하지 않음.



x와 y 스케일도 다르고, 데이터도 늘어진 상태. normalization이 필요한 경우.

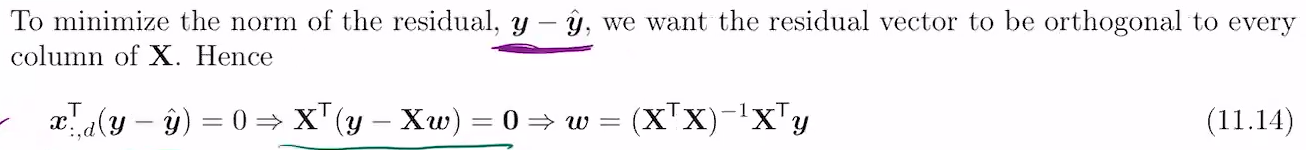
Lasso regression
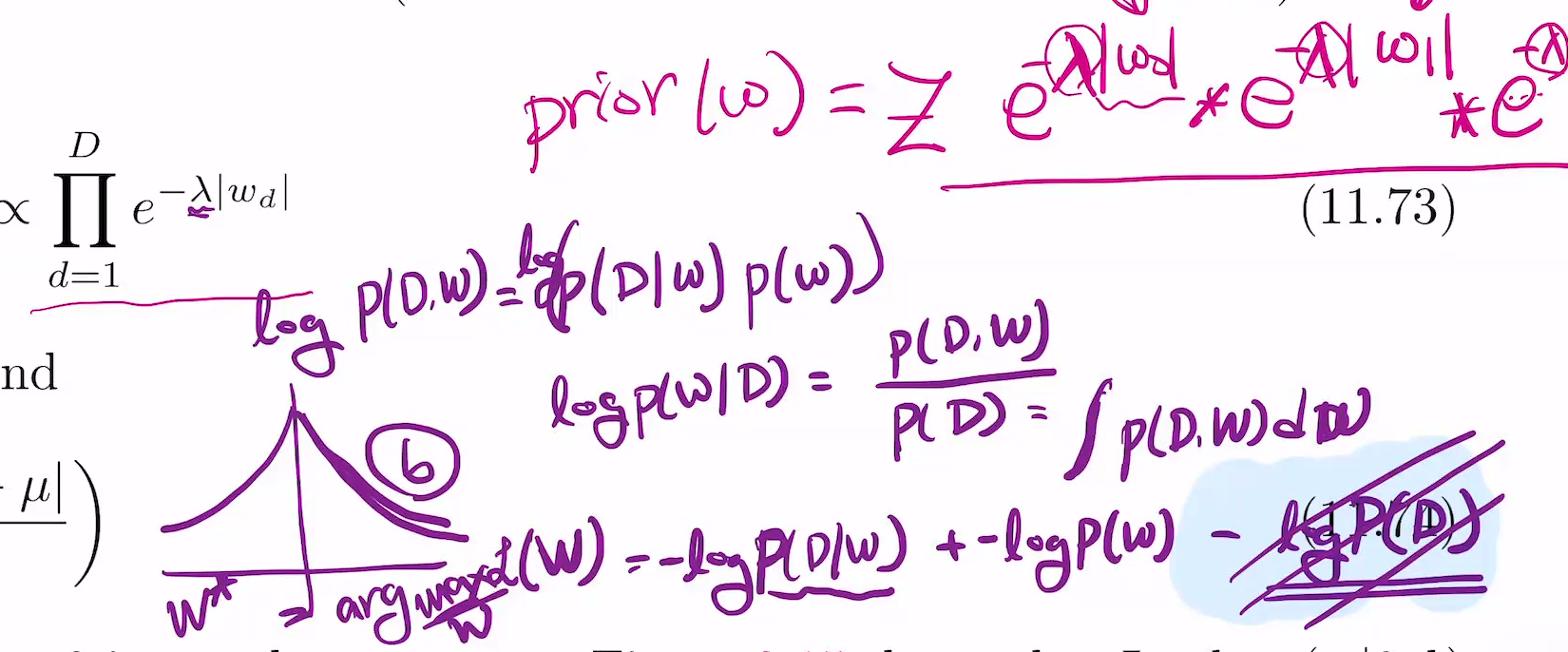
w에 대해 maximize 해야 하는데(w*구할때) 뒤의 텀은 w에 대한 게 없으니 constant라 빼도 됨.
Maximize가 아니라 minimize같으면 -를 붙인 -log p(d\w).
likelihood에 log를 씌우면 앞의 constatnt 없어지고, expotential 안에 있던것만 남게되니, 그게 |Xw-y|2
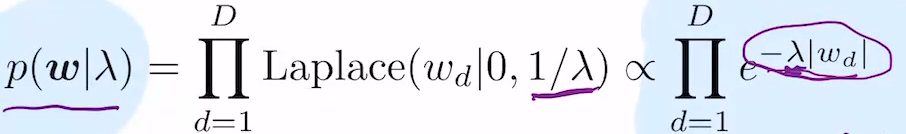
p(w|감마)를 쓸 때 펑션폼은 맨 오른쪽. 그리고 그 e위에 있는거는
w1~wd를 하나의 벡터로 볼때 w벡터의 1norm은 |w1| + |w2| + ... |wd|
이렇게 되면, 여기에 맨 앞에 람다 곱해두면 e^-람다|wd|임. 따라서 loss펑션은
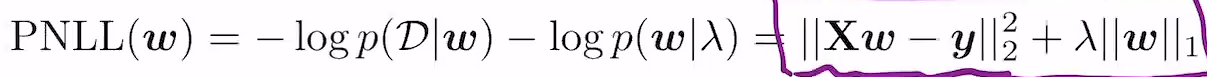
가 됨.
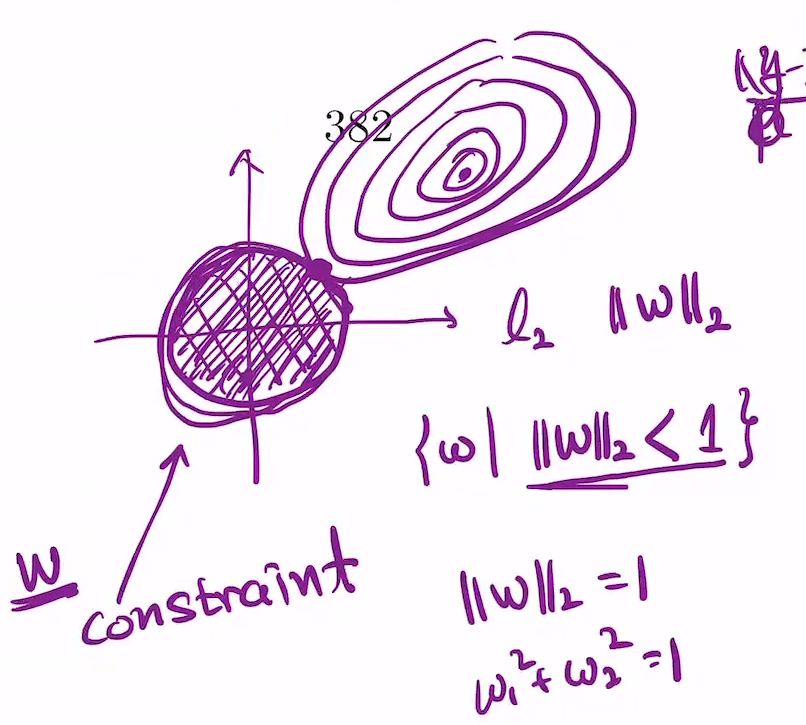
이를 기반으로 그리면

베이지안 선형회귀
가우시안을 쓰면 posterior을 공식으로 구할 수 있음.
각각의 용어는 오른쪽

그리고 포스테리어는

이 xi로부터 평균이 나오고, sigma는
y2의 density는 p(y2|...)

가 되니, 3개라 하면 이 3제곱에 log 씌우고 -1/2.. 등을 진행하면 summation 1~3 하면

의 형태를 띰.
그래서 포스테리어는 아래와 같이 됨.
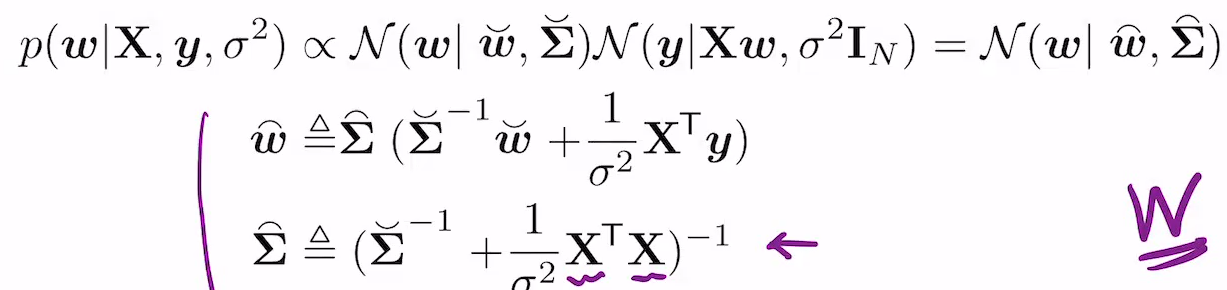
이는 아래에서 기원.



posterior mean인 mu hat t x,
posteriro coviariance인
sigma hat ^2 (x)

좌측의 맨 첫번째 그림은 wt의 w에 대한 그림, 그리고 이게 parameter w 인 likelihood.
prior과 likelihood 합치면 두 번째 posterior 나오고, 이것과 두번째 likelihood 합치면 세번째 posterior 나오고... 이런 관계


Beta prior을 하게 되면 posterior도 beta가 나온다.
Linear Regression and Bayesian


x가 주어지먼 뮤로부터 y방향으로 가우시안 디스트리뷰션 발생.
나의 메저멘트의 위치는 여기다... 모든 x에 대해 이를 진행
이 때 distance줄이기가 목표.
그리고 중심을 이으면 녹색 선이 됨.
이 때, x->N(뮤, 분산) ~ y



앞의건 full rank가 안 될 수 있음(xtx).
뒤의 건(람다 Id, 이 떄 랭크=디=풀랭크)
그래서 람다가 인버스로 계싼하기에 stabliize역할 함.
Lasso regression : sparse estimation 시 사용

여기서 L1 Regualzation은
prior을 뭐로 잡는가?

라플라스 예측

prior = beta fucntion이고 (theta|알파는 2, 베타는 2). 이 떄 베타펑션폼은

이고, likelihood는 베르누이(y|세타) = 세타^y * (1-세타)^1-y
이 떄, D = {0}임
p(세타, D) = (1-세타) * prior(=세타*(1-세타)/베르누이(2,2)), 이 때 (1-세타)인 이유는 데이터가 0이니까.
포스테리어 p(세타|D) = p(세타, D) / p(D)
p(D)는 인테그랄 (세타 * (1-세타)제곱 / 베르누이(2,2))
이 떄, 베타펑션 정의는 아래와 같음.

따라서 P(D)는

그리고 따라서 p(D)를 쓰는 포스테리어는
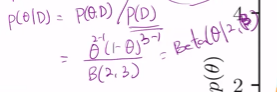
베타 알파는 2, 베타는 3임.
prior은 세타가 0쪽으로 probabilty density가 증가하게 됨.

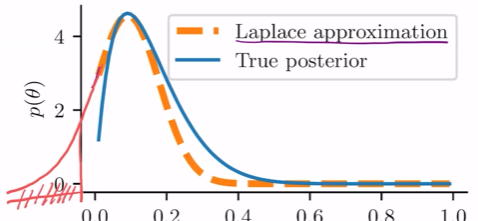
근데 P(D) 적분을 못하면? 이 때 라플라스 예측을 하게 됨.
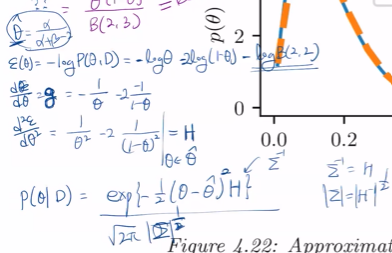
이 때 P(세타|디)가 가우시안 쿼드러틱 예측
체비셰프 부등식 : X가 평균값을 중심으로 하는 베리에이션이 그 확률은 베리언스를 에이제곱으로 나눈 것보다 작음.
이를 기반으로 큰수의 약법칙이 나옴. 샘플의 평균은 덴시티의 평균값에 수렴한다.
clt는 걍 일단 봐라. n이 커질수록 덴시티가 평균분포에 수렴함.

마르코프 부등식

그 증명은 아래.

가 되고
x자리에 a넣으면 a가 가장 작은 숫자.
x는 전체 구간에서 커지고, 여기서 a는 제일 작은 숫자 선택한 것.
그리고 a를 밖으로 내보낸다.
뒤의 a부터 inf까지의 fx적분은
pr[x>=a]
따라서 최종적으로 E[x] >= apr[x>=a]이며 여기에서 a를 서로 나눈 것이 마르코프 부등식임.
체비셰프 부등식
P[|X-E[X]| >= a) <= var(x)/a^2
이는 마르코프 부등식을 활용함.

다음으로 wlln 역시 체비세프 씀.

해당 특성을 활용.
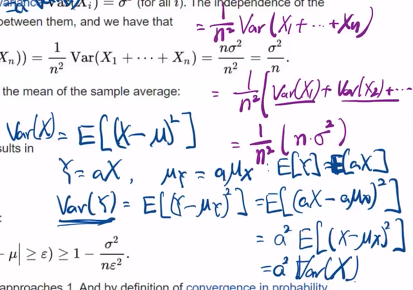
다음을 거치고,
결국은 sigma^2/n이 되는 것.

체비셰프 부등식을 Xbarn에 적용한 것.

이 떄,

입실론을 뭘 주든 간에, n을 충분히 크게 만들면,

중심극한 정리


이 때 ,Sn이 S보다 작아지는 지점..

문제 예제



다음과 같은 리만섬이 있따.
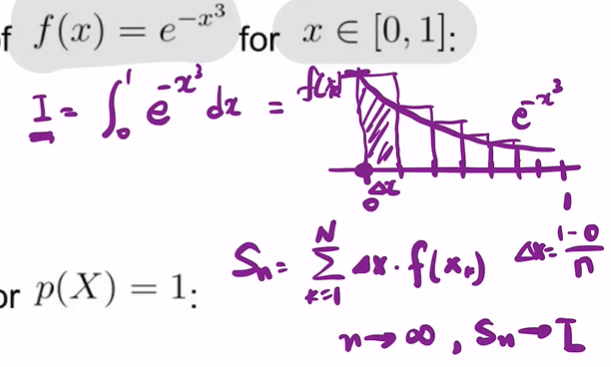
그리고 아래가 있다.

이 떄 샘플 100개를 뽑았따.

그럼 I의 적분은

이렇게 되고,
E[fx]는

이게 몬테카를로 인테그레이션
그리고 몬테카를로 메소드는

그리고


몬테카를로 메소드
iid는 independent identically distribution
이 때, PXY(X,Y)는 PX(X)PY(Y) = (이하 참조)






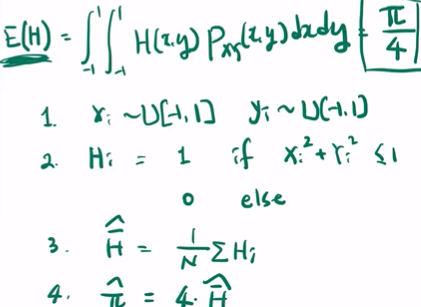
다음과 같이 될 때 필요한 N은? 이건 어려운 문제임
몬테카를로 메소드


n이 커지면 좁아짐(파랑색)
베타펑션에서 샘플을 뽑는다 하자. 그다음 히스토그램 만들면 두 번쨰그림임.
베타처럼 보임.
다섯개를 뽑았다 하자, mean을 구함. 이렇게 batch를 여러개 두고 각자 mean을 구함.
각 mean은 x_5(1), x_5(2), ... x_5(10000)이 됨. 이 평균에 대해 10000개의 샘플을 뽑아 분포를 구하여 히스토그램을 그린 게 세 번째이고, 가우시안 모양이 나오게 됨.
N=50, 즉 위처럼 5개가 아니라 50개씩 뽑는다면? 이렇게 10000번 하여 히스토그램 하면 왼쪽 아래임. 갈수록 가우시안 모양이 됨. 그리고 매우 폭이 좁음. 그 표준편차는 시그마 베타 (1,5)/루트(50=샘플수)


이것의 의의는, 분포를 E로 예측하는 몬테카를로 예측을 쓰자


Laplace Approx - 2
테일러 급수 in one real variable << 전제조건은 미분 가능해야 함.


라플라스 예측은 f(세타)를 -logP(세타)로.
이 떄 q(세타|D)에 EXP가 붙는 이유는 f(세타)에 -log가 있어서.

여기서 끝나지 않고, q(세타|D)를 뭔가로 나눠준다.왜냐? 이거만으론 density가 되지 않기에.
그래서 최종적으론 아래와 같이 됨.

지난 과제 문제 2

이에 대한 답은

이 때, P(D) = integral p(mu, D)du인데 이거 구하긴 어렵다. 따라서

이 떄 뮤 텀이 없는 건 지워지는 것. 저게 0이 된다면, mu hat MAP
세 번째로 헤시안은 한 번 더 미분하는 것. 즉, 원래 식 (1-x)a(1-x)을 x로 두 번 미분하면 a만 남음. 이는 곧
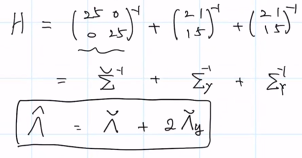
이고, 여기서 muhat MAP는...

인데, 이 두개가 같다는 건
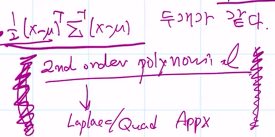
라는 것 이라 함.
1번 문제


이를 기반으로 라플라스 예측을 구하면

이 때, 미분한 값은, 세타를 구해야 할 땐 0으로 설정해야 함.
그리고 중요한 건 네모 친 부분이고 앞 부분은 날려도 됨.

그리고 이 최종식은, 녹색값의 예측임




이 때, 첫 번쨰 그래프에서 0 미만은 어떻게 처리할까? 우선 그 나머지 영역을 고려하자.



여기서 posterior을 모른다 가정. 그렇다면 logit transformation의 joint를 집어넣음.

이걸 활용하면,


이 때, sig(gmaam)(1-sigmoid...) 에 의해, sigmoid는 4승으로, 그 뒤의 것은 5승으로 바뀌게 됨.
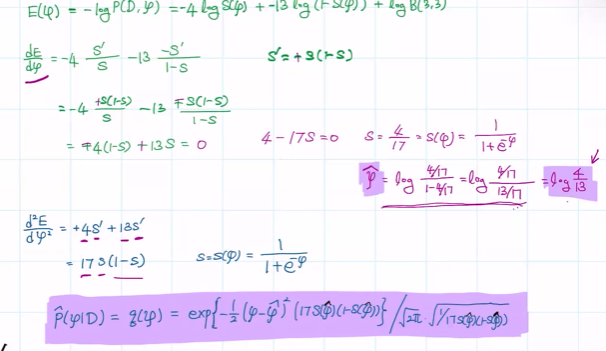
위의 과정을 차용하면,
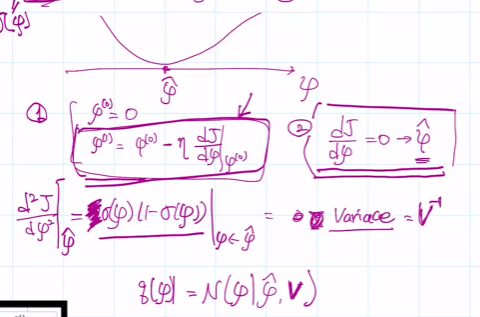
Reparameterization Trick

그 reinforce approximation은

가 됨. 보통 q는 가우시안이고, 여기에 로그를 씌우면 푸른 색의 박스.


이 때, gradient fucntion g(theta)와 몬테카를로method를 적용한 식은

아래의 X는 미분하면 다 없어지는 텀임.
평균계산을 하고 남은 것의 loss fucntion이 Eqtheta[X2]이고, 세타에 대해 minimize 해야 함
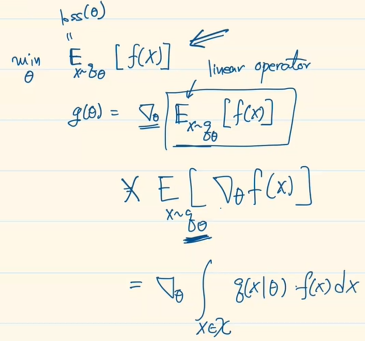
이제 이걸 미분해야 함. 그래디언트 계산을 해야 하니까.

이것이 Reinforce라 하는 방법이고, 아래는 Reparameterization trick


Entropy


maximum entropy를 만드는 경우, uniform-distribution이 됨.

이를 다시 계산시,

4면 주사위 예로 들면




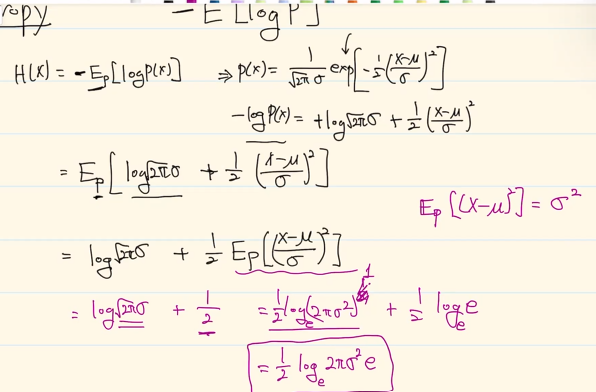
엔트로피에 적분하면?
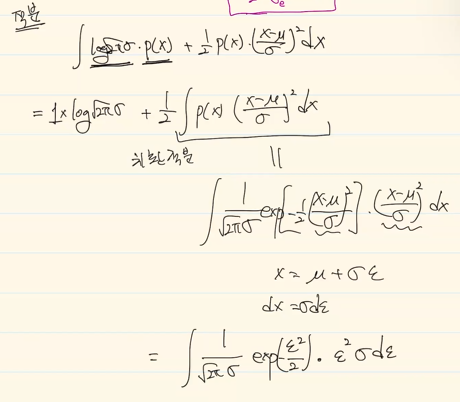
가 되고, 다시

가 됨.
discrete markov chain