* 데이터를 토대로 산출한 모델의 예측값과 실제 값의 차이를 표현
* 회귀타입) 평균오차 계산법, MAE와 MSE, RMSE로 구분됨
1-1) MAE(평균 절대 오차, Mean Absoulte Error)

예측값과 절대값의 차이에 절대값을 취하고, 평균을 낸 간단한 방식
절대값을 취하기에, 음수인지 양수인지 판단이 불가
즉, 어떤식으로 오차가 발생했는지 모름
또한, 최적값에 가까워지더라도, 값에 수렴하긴 힘듬.

1-2) MSE(평균 제곱 오차, Mean Squared Error)

예측값과 실제값 아이의 평균을 제곱해 평균을 냄
차이가 커질수록 값이 뚜렷해지며, 오차가 양수든 음수든 누적값이 증가됨.
최적값에 가까워질 경우, 이동거리의 변화가 유동적이기에 최적값에 수렴하기 쉬우나,
값이 제곱이기에 1 미만의 값은 작아지고, 그 이상의 값은 커지는 왜곡이 발생하기 쉬움.

1-3 ) RMSE(평균 제곱근 오차, Root Mean Square Error)
MSE에 루트를 씌움. 따라서, 값을 제곱해서 생기는 왜곡이 감소함.
*분류타입) Cross-entropy방식이 존재.
실제 분포 q에 대해 알지 못하는 상태에서, 모델링을 통해 구한 분포인 p를 통해 q를 예측

실제값과 예측값이 맞다면 위는 0으로 수렴할 것이고, 그렇지 않다면 커질 것이다.
엔트로피 = 불확실성의 척도. 높을 때 정보가 많고, 확률이 낮다는 것을 의미
예) 동전던지기와 주사위굴리기의 엔트로피는 아래와 같다.

동전의 엔트로피는 약 0.7, 주사위는 1.8로, 주사위의 엔트로피가 더 높으며, 즉 주사위가 불확실성이 더 큼을 뜻함
이것을 그래프로 표하면

위에서, p(xi)는 각 요소가 나올 확률값이며, 모두의 총값은 1이다.
모든 요소가 나올 확률이 같다면, -logp(xi)의 값도 동일하다.
따라서, 아래의 식이 성립

이 시그마 옆의 p(xi)를, 현재 알지 못하는 실제분포 q로 바꾼 것이 곧 크로스엔트로피.
https://westshine-data-analysis.tistory.com/m/83#:~:text=%E2%96%B6%ED%81%AC%EB%A1%9C%EC%8A%A4%20%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BC%EB%9E%80&text=%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BC%EA%B0%80%20%EC%A0%95%EB%8B%B5%EC%9D%B4%20%EB%82%98%EC%98%AC,%EC%9E%88%EB%8A%94%20%EC%A0%95%EB%B3%B4%EB%9F%89%EC%9D%84%20%EC%9D%98%EB%AF%B8%ED%95%9C%EB%8B%A4.
2-1) Binary Cross Entropy

이진분류에 사용된다.
예측값이 0과 1 사이의 확률값으로 나오며, 클수록 T에 가깝다.
2-2) Categorical Cross Entropy

멀티클래스에서 라벨이 One-hot 인코딩 방식으로 제공될 때 사용
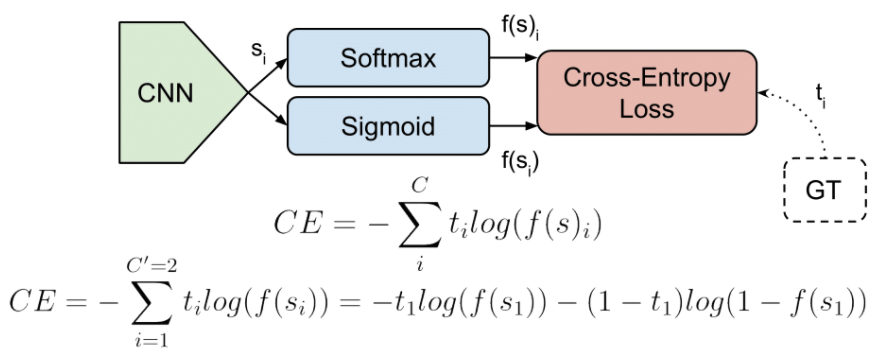
이 때, Cross Entropy Loss를 더욱 알아보면,

위처럼, Linear Model을 통해 최종값(Logit)을 내고, 이를 softmax를 통해 0~1 사이의 값으로, 총합을 1이 되도록 한다.
다음으로, 1-hot label과 Cross Entropy를 통해 Loss를 구한다.
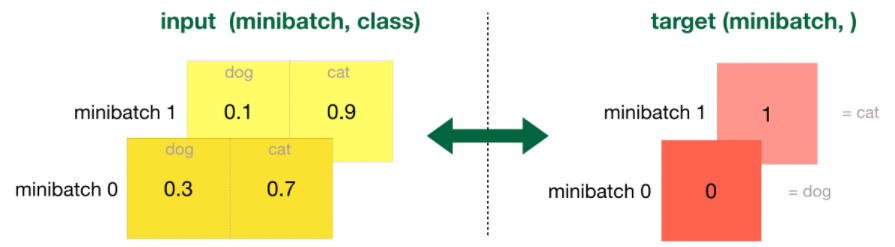
CrossEntropyLoss 함수는 input tensor size는 (minibatch, class)이며
class의 range는 [0, C-1]이다.
target shape는 (minibatch,)이며, 이때 target[i]의 range는 [0, C-1]이다.
정답클래스에 해당되는 스코어에 대해서만 로그합을 구해 최종 Loss를 구한다.
BCELoss는 Binary Class Enropy Loss 함수의 준말. 즉, cross entropy를 구하며,
여기에 softmax같은 activation func을 따로 적용하여,
input과 target은 (minibatch, ) shape를 갖게 되고,
각 minibatch마다 input값의 range는 [0,1]이 되며, target값은 0이나 1이 나오게 됨.
출처, 참조한 글
https://nuguziii.github.io/dev/dev-002/
https://brunch.co.kr/@mnc/9
http://melonicedlatte.com/machinelearning/2019/12/20/204900.html
'버츄얼유튜버' 카테고리의 다른 글
| 비전 1) 봐두면 좋은 논문 및 긍/부정 부류, DB (0) | 2021.12.13 |
|---|---|
| GAN의 G와 D 객체 (0) | 2021.12.13 |
| 6.푸리에변환 3 & 편미분방정식 (0) | 2021.12.13 |
| 5.푸리에 변환2 (0) | 2021.12.13 |
| 공학수학 4.푸리에변환 (0) | 2021.12.01 |

