모라벡 알고리즘

제곱합의 오차를 이용, 특징점으로 확률이 높은 픽셀엔 높은 값을, 낮은 픽셀엔 낮은 값을 부여
이중 최소값을 특징가능성값으로 판단
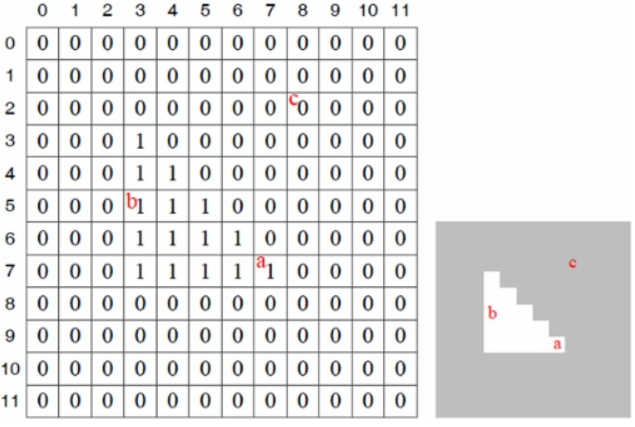
위의 이미지에서, b(5,3)을 조사한다 가정하고 제곱차합을 계산한다.
이때, 마스크는 3*3의 1로만 이뤄져있다.

오른쪽으로 한 화소만큼 이동시킨 S(0,1)의 값은 4이다. 이외의 a,b,c 세 지점에서 S(u,v)를 구하면

화소 b는, 에지는 세로방향인데 그 방향으로는 낮은값을 가지나, 에지와 수직인 가로방향은 크다.
화소 a는, 물체의 코너에 해당하며, 모든 방향에서 큰 값을 갖는다.
즉, 제곱차의 합은 어떤 점이 다른 곳과 얼마나 두드러지게 다른지 측정
물체의 코너는 두드러지게 다르기에, 이 S를 코너일 가능성으로 추정이 가능하다.
해리스 코너
모라벡은, 한 화소만 동서남북으로 이동시키는 방식이므로, 나머지방향으로는 대처가 불가하다.
이를 미분을 통해 해결한다.

한 픽셀을 중심에 두고, 마스크를 설정한 다음 x축으로 u, y축으로 v만큼 이동시킨다 하자.
이게 바로 위에서 적은 모라벡 코너인데, 이는 테일러확장과 도함수에 의해 다음과 같이 근사된다.

그냥 식을 풀어쓴 다음에 u와 v에 도함수 붙인거임.

이를 행렬로 나타내면 위처럼 되는데 이 행렬을 고유값 분해를 통해 고유 벡터의 획득이 가능하다.
두 고유값 중, 더 큰 고유값과 연결된 고유벡터의 방향으로 이미지변화가 가장 크다.
즉, 두 방향으로 변화가 크면 코너점이며, M의 고유값이 충분히 크다.
하나만 크고 하나만 작다면 이는 엣지이다.

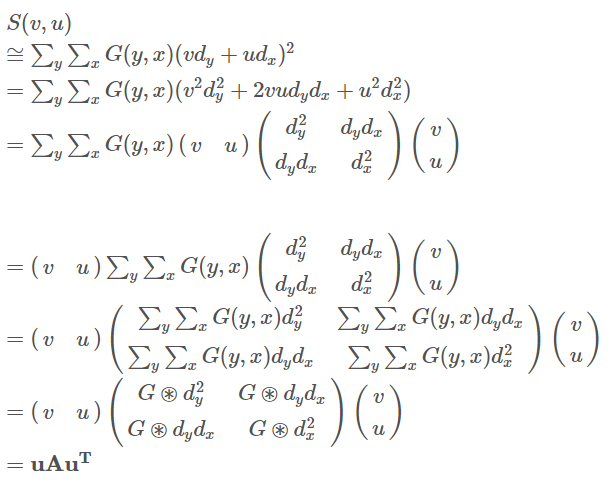
풀이하면 위와 같이 되며, A가 2차 모멘트 행렬이 된다.

c의 경우, 두 개의 고유값 모두 0에 가까운, 변화가 없는 곳
b의 경우, 한 방향으로만 에지가 있는, 고유값이 하나만 큰 곳
a의 경우, 두 고유값이 다 큰, 여러 방향으로 변화가 있는 코너
해리스 코너 (Harris corner) · Monch
해리스 코너 (Harris Corner) 해리스는 모라벡의 마스크를 중심에서 멀어질수록 서서히 값이 작아지는 가우시안 마스크 G(x,y)로 대치하였다. 이렇게 해서 Sum of Squared Difference(SSD)는 다음의 가중치 제
songminkee.github.io
2차 미분 활용
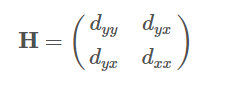
미분은 잡음을 증폭시킨다는 점이 있다. 따라서, 우선 미분을 한 다음 가우시안 스무딩을 거친다.

예를 들어, dyx(o)는 입력영상 f를 o크기의 가우시안필터 G로 컨볼루션한 후, 그 결과를 y방향으로, 다음으로 x방향으로 미분한 도함수
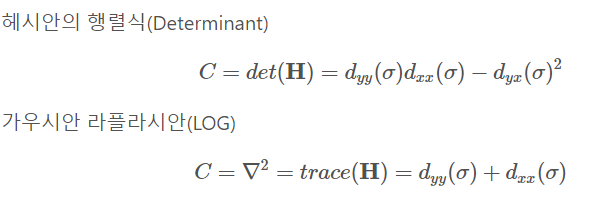
SUSAN
현재 처리 중인 중심점과, 인근 지역의 밝기값이 얼마나 유사한가 따지고, 그 결과에 따라 특징일 가능성을 측정
USAN(우산)이라 하는, 중심점에 원형 마스크를 씌우고 중심점과 명암값이 유사한 점으로 구성된 영역을 이용,
마스크와 우산의 크기 비율을 측정한 후, 50%정도인 곳이 에지, 작은 곳이 코너로 검출

usan_area가 중심점 r0에서의 USAN의 크기, r은 원형마스크 내의 화소
다음으로, USAN의 크기를 특징 가능성으로 표현하는 식은 아래와 같다.

위 경우, 보통 f2는 보통 마스크 넓이의 50%로 설정하고, q는 마스크넓이의 75%배로 설정한다.
비최대 억제
코너에서 한 점만 큰 값을 갖는것이 아닌, 큰 값이 일정한 범위에 퍼져있어 한 점을 선택하는 방법이 필요할 때, 위치 찾기(Localization)을 쓴다.
보통 지역 최대점을 선택하는데, 지역 내에서 최대일 때 특징점으로 결정되는 것.
이 때, 적응적 비최대 억제 방법이라는, '특징점이 영상의 특정부분에 밀집되어 있고, 다른 부분은 드물게 분포하는' 문제점에 대한 해결책으로 특징점이 지역 내에서 최대이며, 주위 화소보다 일정 비율 커야 하는 조건부 방식이 생김.
def NMS(feature,n=4,threshold=0.02):
feature = np.expand_dims(feature,-1)
# 상하좌우
n_r = np.pad(feature[1:], ((0, 1), (0, 0),(0,0)))
n_l = np.pad(feature[:-1], ((1, 0), (0, 0),(0,0)))
n_d = np.pad(feature[:,1:], ((0, 0), (0, 1),(0,0)))
n_u = np.pad(feature[:,:-1], ((0, 0), (1, 0),(0,0)))
if n==8: # 대각선
n_ul = np.pad(n_u[:-1], ((1, 0), (0, 0),(0,0)))
n_ur = np.pad(n_u[1:], ((0, 1), (0, 0),(0,0)))
n_dl = np.pad(n_d[:-1], ((1, 0), (0, 0),(0,0)))
n_dr = np.pad(n_d[1:], ((0, 1), (0, 0),(0,0)))
ret = np.concatenate([feature,n_r,n_l,n_d,n_u,n_ul,n_ur,n_dl,n_dr],axis=-1)
else:
ret = np.concatenate([feature,n_r,n_l,n_d,n_u],axis=-1)
ret = np.expand_dims(np.argmax(ret,-1),-1) # 최대값을 가지는 index
return np.squeeze(np.where(np.logical_and(ret==0,feature>threshold),feature,0)) # ret이 0 이라는 것은 지역보다 크다는 것을 뜻한다.https://songminkee.github.io/studyblog/computer%20vision/2020/08/24/non_maximum_suppression.html
비최대 억제(Non-Maximum Suppression) · Monch
코드링크 비최대 억제(Non-Maximum Suppression) 이전에 포스팅한 모라벡, 해리스, 헤시안 행렬, 슈산 모두 어떤 점에 대해 특징일 가능성을 측정해주었다. 하지만 코너에서 한 점만 큰 값을 갖는 것이
songminkee.github.io
스케일에 불변한 특징점 검출
다른 크기의 같은 사진은, 하나의 봉우리도 큰 사진에선 여러 곳에서 특징점이 검출되지만, 작은 사진에선 검출량이 적을 수 있다.
따라서, 스케일에 불변한 특징점 검출이 필요하다.
다중 스케일 영상 구축에는 2가지 방법이 존재하는데,
첫번째는 가우시안 스무딩을 이용
두번째는 이미지 피라미드를 구축하는 방법
그러나 현실에서는 연속적으로 스케일이 변화하나, 피라미드 방식은 스케일이 두배씩 줄어드는 한계를 가져
가우시안 스무딩 방식이 주로 사용됨.
가우시안 스무딩은 표준편차로 스케일을 조정하며 키움으로서, 물체를 멀리 떨어트려 보는것과 비슷한 효과를 냄
가우시안을 이용해, 분산이 커질수록 영상의 스무딩 효과는 커진다. 이를 통해 다양한 영상을 획득하여, 스케일 효과를 준 '다중 스케일 영상'을 구축했다. 그렇다면 지역 극점을 찾을 차례이다.
다중 스케일 영상에 정규 라플라시안(라플라시안에 pow(분산,2)을 곱한 것)을 적용한다.
dyy와 dxx는 분산값이 클수록 작아지기에, 정규화를 하여 0~1사이에서 보기 편하도록 할 필요가 있다.
dyy(var)은, 영상 f에 크기가 var인 가우시안으로 스무딩을 하고 y방향으로 2번 미분한 식이다.
이 때, 교재를 보면 작은 블롭은 var=3.59에서 극점이 발생한다.
또한 큰 블롭 역시 극점이 var=5.50에서 나타난다.
한데 두 블롭은 1.57배이고, var의 두 극점의 비율은 5.5/3.59=1.53이므로 매우 유사하다 할 수 있다.
이를 활용해, 여러 크기의 분산을 적용해 3차원 스케일공간을 구성하고, 그 공간에서 극점을 찾으면 큰 물체와 작은 물체 모두에서 특징점을 찾을 가능성이 확보된다. 거기에 더불어, 이는 스케일 정보도 지니고 있다.
해리스 라플라스 검출
그렇다면 3차원 공간에서는 어떻게 극점을 찾을까?
영상 공간 (y,x)와 스케일축 t 각각에서 잘 작동하는 식을 사용하여,
영상공간에서는 해리스의 식을, 스케일 축에서는 정규 라플라시안 식을 사용하면 됨.




SIFT
Lowe99, Lowe2004에서 발표됨
피라미드 + 가우시안 구조 && 각 층 여섯 영상의 묶음(옥타브)로 구성 && 각 옥타브 영상은 σi로 스무딩
1) 피라미드를 만든다. 원본 이미지를 점진적으로 블러, 원본을 두 배로 한 다음 블러, 반으로 한 다음 블러...
by 가우시안 연산자와 이미지를 컨볼루션 연산. σ를 점차 k배씩 높여감으로써 가능하다.
이렇게 만들어진 같은 사이즈의 블러처리된 것들을 옥타브라고 한다.

2) 다양한 scale값으로 가우시안 연산처리된 서로 다른 4개의 사이즈의 블러가 각 처리된 5개(총 20) 이미지를 획득.
이 때 Laplacian of Gaussian(LoG)나 Difference of Gaussian(DoG)를 사용하면, keypoint 획득이 가능.
이미지 내에 있는 엣지 및 코너가 두드러지게 되는데, 전 단계에서 얻은 같은 옥타브 내의 인접한 2개의 블러 이미지를 빼면 된다.

3) 오른쪽에, 이미지 엣지 정보가 도출된 것을 볼 수 있다.
이제 DoG에서 키포인트를 찾는다. 각 이미지 내의 극대값, 극소값 위치를 찾으면 된다.

체크할 DoG이미지와, 스케일이 한단계씩 크고 작은 이미지를 보자.
총 27개 중, 체크할 것을 제한 26개를 검사한다. 만일 현재 체크하는 픽셀의 값이 26개의 이웃 픽셀값 중 가장 작거나 클 때 keypoint가 된다. 즉, DoG 중 가장 위와 가장 밑에 있는 옥타브 이미지는 극대(소)값 검출이 불가

4) 이렇게 얻은 점이 1차 keypoint. 5장의 블러 이미지에서 4장의 DoG이미지가 나오고, 여기에서 2개의 극값이미지 검출. 이렇게 20장을 이용하면 총 8개의 극값이미지를 획득하게 된다.
그러나 극대, 극소값은 픽셀과 픽셀 사이에 존재할 가능성이 있기에, 이러한 subpixel에 접근하기 위해, 테일러2차전개를 활용한다.


5) 활용가치가 떨어지는 keypoint를 제거한다.
우선, 낮은 콘트라스트를 제거 & 엣지 위에 존재하는 것 제거
낮은 콘스라스트 == DoG이미젱서 keypoint의 픽셀의 값이 특정 threshold보다 작으면 제거한다.
다음으로, 수직(수평)으로만 변화가 크고, 반대로는 변화가 없는 엣지를, 각 keypoint의 수직, 수평 그래디언트를 계산함으로써 알아낸 다음 제거한다.
6)그럼, 이 keypoint에 방향을 할당한다. 이 keypoint는 스케일 불변성을 지니기에, 방향을 할당함으로써 회전 불변성을 줄 수 있다. 각 keypoint 주변의 그레디언트 방향과 크기를 모아, 두드러지는 방향을 찾아 keypoint방향으로 할당한다. 이 keypoint의 scale값으로 가우시안 블러링을 한다.
다음으로, 그 안의 모든 픽셀의 그레디언트 방향과 크기를 구한다.

이제 이 keypoint에 방향을 할당한다. 그레디언트 크기에 가우시안 가중함수를 이용해, keypoint에 가까울수록 더 큰값을, 멀수록 작은값을 갖게 하는데, 다음으로 히스토그램을 36개 만든 다음 각 360도를 36개로 10도씩 쪼개는 것이다.
즉, 만일 55도라면, 3번째 히스토그램에 그래디언트크기만큼 합한다. 이렇게 해서, 그래디언트 방향에 대한 히스토그램이 완성되면, 가장 높은 bin의 방향이 keypoint 방향으로 할당된다.
7) 각 keypoint의 특징을 128개의 숫자로 표현한다. 이를 위해, keypoint 주변에 16*16의 윈도우를 세팅하고, 다시 4*4로 나눈다.
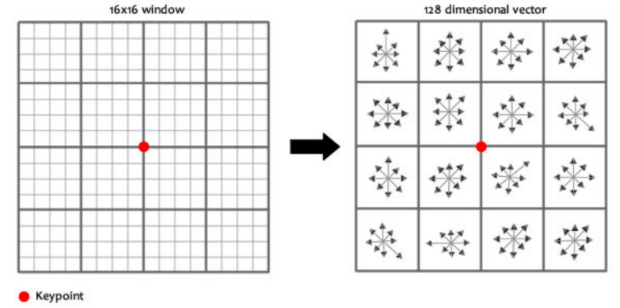
각 윈도우에 속한 픽셀의 그래디언트 크기와 방향을 계산한다. 단, 이번엔 bin을 8개로 나눈다.
이렇게 해서 채우고 나면, 8*16개의 벡터가 생성될 것이다. 이를, 회전 불변성으로 만들기 위해, key point의 방향을 각각의 그레디언트 방향에서 뺀다. 그럼 각 그레디언트 방향은 keypoint의 방향에 상대적이게 된다.
예) keypoint의 방향을 구한 것이 20-29도라면, 24.5도를 keypoint 주변 16개의 4x4 윈도우의 방향에서 빼주면, 16개의 윈도우의 방향은 keypoint 방향에 상대적이게 됨.
밝기 불변성을 위해, 정규화를 시킨다.
이렇게 획득한 keypoint에게 지문(위에서 구한 값들)을 할당하면 된다.
마지막으로, 두 이미지에서 각 keypoint를 찾고 지문값을 달았다면, 이 차이가 가장 작은 곳이 매칭되는 위치.
쓰면서도 알쏭달쏭 이해가 될거같기도 한데 수식이 왜 도출되는지 알수없네
[튜토리얼논문]
Tuytelaars2007

이 떄, dyy를 근사화한 연산자 Dyy를 빠르게 계산하기 위해, 적분 영상을 이용한다.

위 영상의 일부를 합한 부분합은 간단한 식으로 계산이 가능할 것이다. 가령 오른쪽 하단 4칸의 1, 1, 1, 0의 합은 3이다.
이 범위는 총합인 21에서 윗부분인 11과 좌측인 11을 뺀 다음, 중복되는 부분인 4를 더함으로써 3이 완성되는 것으로 구할 수 있다.

피라미드를 구축하기 위해 가우시안 스무딩을 하는 SIFT와 달리, SURF는 원본 영상을 그대로 둔 채 근산연산자의 크기를 조절해 스케일 공간을 구축한다.
다음으로, 헤시안을 이용해보자. determinant(행렬식)이 음수이고, 고유값과 서로 부호가 다르면 해당 좌표는 관심점이 아니다. 둘 다 양수 혹은 음수여야 관심점으로 판단된다.
SIFT의 1, 2번 과정에서 가우시안 연산자를 쓴다 했는데, 반대로 SURF에서는 위처럼 근사화한 연산자를 활용, 적분 이미지 계산으로 영역의 넓이를 구한 다음 그 넓이로 헤시안 행렬을 계산해 관심점을 판단한다.

한 이미지에 σ를 N배 늘리면 N배의 이미지가 나오게 된다. 이렇게 연산자를 키워가며 다양한 크기의 연산자를 만든다.
이를 원래 영상에 적용해, 여러 개의 스케일에 해당하는 영상 집합을 만든다.
각 스케일에서 헤시안의 행렬식을 적용해 행렬식 영상을 만든다.

다음으로, 이 행렬식 영상은 하나의 옥타브를 형성하는데, 중간 사이즈의 연산자로 만든 두 영상에 대해 SIFT에서 활용한 DoG 맵에서의 키포인트 검출(Sift의 3번)을 통해 지역 극점을 검출한다.
"""
하나의 스도쿠를 이진화 통해 하얗게, 까맣게 해서,
에지를 검출해서 칸을 본다
필기를 인식해서 숫자를 보고 빈 부분에 숫자를 넣는 것도 가능할지도....
"""
정리
1) 지역특징의 성질은 특징 벡터의 추출 단계는 불변이어야 한다. 또한, 물체가 이동이나 회전, 스케일이 달라지면 그에 따라 위치, 스케일, 방향도 변해야 하기에, 공변해야 한다.
2) 모라벡 알고리즘은 이동과 회전에 불변한 특징점 검출.
2-1) 한 영역을 제곱합의 오차와 3x3 마스크를 통해, 네 방향의 변화가 다 크면 특징가능성이 높다고 본다.
3) 해리스 코너는, 모라벡의 4방향만 살피는 단점에서 착안,
3-1) 한 픽셀을 중심에 놓고 작은 윈도우(window)를 설정한 후에, 이 윈도우를 x축 방향으로 u만큼, y축 방향으로 v만큼 이동시킨다.
3-2) 윈도우 내의 픽셀 값들의 차이의 제곱의 합을 구해, 두 방향으로 변화가 크면 코너, 하나의 고유값은 크고 다른 고유값은 작다면 엣지
4) 스케일에 불변한 특징점 검출, SIFT와 SURF
5) SIFT
5-1) 원본 이미지를 가우시안 연산자와 컨볼루션 연산 등을 통해 점진적으로 블러, 원본을 두 배로 한 다음 블러, 반으로 한 다음 블러... 시켜 피라미드를 만든다.
5-2) 다양한 scale값으로 가우시안 연산처리된 서로 다른 사이즈의 블러시킨 이미지를 획득했으니,
전 단계에서 얻은 같은 옥타브 내의 인접한 2개의 블러 이미지를 빼서, 엣지 및 코너가 두드러지는 keypoint를 획득한다.
5-3) 이미지 내의 극대값, 극소값 위치를 찾고, 극값 이미지를 얻는다.
5-4) 이 keypoint에, 각 keypoint 주변의 그레디언트 방향과 크기를 모아, 두드러지는 방향을 찾아 keypoint방향으로 방향을 할당한다. 이 keypoint는 스케일 불변성을 지니기에, 방향을 할당함으로써 회전 불변성을 줄 수 있다.
5-5) 그 안의 모든 keypoint의 그레디언트 방향과 크기를 구한다.
5-6) 이렇게 되면, keypoint descriptor라고 하는, keypoint의 특징을 16개의 box * 8방향 = 128개의 숫자로 표현한다. 이를 위해, keypoint 주변에 16*16의 윈도우를 세팅하고, 다시 4*4로 나눈 다음, 각 윈도우에 속한 픽셀의 그래디언트 크기와 방향을 계산한다.
5-7) 이렇게 해서 채우고 나면, 8*16개의 벡터가 생성될 것이다.
5-8) 밝기 불변성을 위해, 정규화를 시킨다. 이렇게 획득한 keypoint에게 지문(위에서 구한 값들)을 할당하면 된다.
5-9) 두 이미지에서 각 keypoint를 찾고 지문값을 달았다면, 이 차이가 가장 작은 곳이 매칭되는 위치.
6) SURF
6-1) 적분합 이용
6-2) 피라미드를 구축하기 위해 가우시안 스무딩을 하는 SIFT와 달리, SURF는 원본 영상을 그대로 둔 채 근산연산자의 크기를 조절해 스케일 공간을 구축
6-3) SIFT의 1, 2번 과정에서 가우시안 연산자를 쓴다 했는데, 반대로 SURF에서는 적분 이미지 계산으로 영역의 넓이를 구한 다음 그 넓이로 헤시안 행렬을 계산해 관심점을 판단
6-4) 연산자를 키워가며 다양한 크기의 연산자를 만든다. 이를 원래 영상에 적용해, 여러 개의 스케일에 해당하는 영상 집합을 만들고, 각 스케일에서 헤시안의 행렬식을 적용해 행렬식 영상을 만든다.
6-5) SIFT에서 활용한 DoG 맵에서의 키포인트 검출(Sift의 3번)을 통해 지역 극점을 검출
'버츄얼유튜버' 카테고리의 다른 글
| 비전 6) 특징기술 (0) | 2021.12.28 |
|---|---|
| 비전 5) 영상 분할 (0) | 2021.12.28 |
| 비전 임시) 얼굴, 눈 검출 (0) | 2021.12.16 |
| 비전 3) 에지 검출 (0) | 2021.12.15 |
| GAN) batch normalization (0) | 2021.12.14 |


