1. 개요
본 논문 - 다단계 네트워크에서 멀티스케일 기능 표현을 활용하여 크라우드 카운팅에서 대규모 변동 문제를 해결. Specific Feature Level은 특정 범위의 스케일에서 더 나은 성능을 발휘하는 경향이 있기 때문에, 적절한 기능 수준 선택 전략(proper feature level selection strategy)으로 이미지패치의 계수 오류(coutning error)를 가능한 한 작게 유지하는 방식으로 해당 아이디어를 구현한다.
그러나 스케일의 주석이 없으면 스케일이 다른 머리에 대한 예측을 specfic feature levels에 수동으로 할당하는 것이 차선이며 오류가 발생하기 쉽다. 따라서 스케일과 feature level 간의 internal correspondence을 자동으로 학습하는 스케일-적응형 선택(Sclae-Adaptive Selection) 네트워크(SASNet)를 제안한다.
SASNet은 가장 적절한 기능 수준의 예측을 최종 추정으로 직접 사용하는 대신 가중 평균을 통해 다른 feature level의 예측을 고려하여 이산 기능 수준과 지속적인 스케일 변동 간의 격차를 완화하는 데 도움이 된다. 로컬 패치의 헤드는 대략적으로 동일한 스케일을 공유하기 때문에 패치별 스타일로 적응형 선택 전략을 수행한다. 그러나 패치 내의 픽셀은 다양한 학습 난이도로 인해 서로 다른 카운팅 오류를 일으킨다. 따라서 픽셀 수준에 도달할 때까지 패치 내에서 가장 단단한 하위 영역을 재귀적으로 선택하는 피라미드 영역 인식 손실(PRA 손실)을 추가로 제안한다. 상위 패치가 과대 추정되었는지 과소 추정되었는지에 대한 인식으로 이러한 지역 인식 하드 픽셀에 대한 PRA 손실을 통한 세분화된 최적화는 훈련 대상과 평가 메트릭 간의 불일치 문제를 완화하는 데 도움이 된다.
2. 소개
군중 계수는 주어진 이미지 또는 비디오 내의 사람 수를 추정하는 것을 목표로 한다. 대부분의 최신 연구는 딥 러닝 기반 방법을 채택하고 사람 머리의 중심점을 훈련 대상으로 밀도 맵으로 변환한다. 그러나 이 작업의 주요 과제는 군중의 극단적으로 큰 규모의 변화이며, 스케일 주석의 부족으로 인해 훨씬 더 까다로워진다. 최근 몇 년 동안, 군중 계수의 대규모 변동 문제를 해결하기 위해 수많은 방법이 제안되었다. 실현 가능한 해결책 중 하나는 다양한 수용 필드(receptive field)를 가진 여러 분기를 집계하여 풍부한 스케일 정보를 가진 기능을 획득하는 다중 열 네트워크를 사용하는 것이다. 그러나 이러한 방법은 연속적인 스케일 변동을 다룰 수 없으며, 이로 인해 서로 다른 분기 간에 feature 중복(feature redundancy)이 발생한다. 다른 주요 접근 방식은 모든 feature level의 활용에 의해 최종 예측이 생성되는 다단계 네트워크를 채택한다. 그러나 이러한 방법은 feature level과 헤드 스케일 간의 본질적인 대응을 무시하는 스케일에 구애받지 않는 방식으로 여러 수준의 기능을 집계한다. 일반적으로 이 두 가지 방법은 다중 스케일 기능 표현의 이점을 얻지만, 두 가지 모두 이러한 풍부한 스케일 정보를 효과적으로 활용하지 못한다.
본 연구에서는 다중 스케일 기능 표현을 최대한 활용하기 위해 새로운 다단계 기반 스케일 적응 선택 네트워크(SASNet)를 제안한다. SASNet은 추가 스케일 주석 또는 스케일 추정 전략을 사용하지 않고 내부 레벨 스케일 대응을 자동으로 학습하는 적응형 선택 전략을 채택한다. 특히, 주어진 이미지 패치에 대해 SASNet은 각 feature level에 대한 점수를 예측하여 가장 적합한 수준이라 도출한다.
그런 다음 이러한 점수를 가중치 계수로 정규화하고, 이를 사용하여 모든 feature level에서 예측 밀도 맵의 가중치를 다시 부여한다.
마지막으로, 이미지 패치에 대한 최종 예측은 재가중 예측을 합산하여 얻어지며, 이는 이산 기능 수준과 지속적인 스케일 변동 간의 불일치를 줄이는 데 도움이 된다. 적응형 선택 전략은 Feature level과 Head Scale 사이의 Internal Correspondence을 합리적으로 학습한다. 제안된 적응형 선택 전략은 패치의 헤드에 대한 패치별 기능 수준 선택을 가능하게 하지만 패치 내 픽셀에 대한 다양한 학습 난이도를 무시한다. 반대로, 각 기능 수준의 학습은 픽셀 단위 회귀 손실에 의해 유도되며, 이는 분명히 지역적으로 무지하다.
패치 내의 픽셀을 세분화된 방식으로 더욱 최적화하기 위해 새로운 피라미드 영역 인식(PRA) 손실을 제안한다. PRA 손실은 픽셀 수준에 도달할 때까지 과대평가(또는 과소평가)된 패치에서 가장 과대평가(또는 과소평가)된 하위 영역을 재귀적으로 검색한다. 검색 프로세스 후, 이러한 영역 인식 픽셀은 추가로 최적화될 가장 어려운 샘플로 선택된다. 게다가, 널리 채택된 훈련 손실은 정확한 픽셀 단위 회귀를 강조하는 반면, 평가 메트릭은 지역의 군중 수에만 초점을 맞춘다. 결과적으로, 픽셀과 영역 사이의 포함 관계를 고려한 후, 우리의 PRA 손실은 또한 훈련 대상과 평가 메트릭 간의 불일치를 줄이는 데 도움이 된다. 결론적으로 본 연구의 기여는 다음과 같이 요약된다.
1. 우리는 가장 적절한 기능 수준을 식별하기 위한 패치별 기능 수준 선택 전략을 제안한다. 이러한 새로운 전략은 다단계 네트워크 내의 다중 스케일 기능 표현을 효과적으로 활용하여 도전적인 대규모 변동 문제를 해결하는 새로운 방법을 제공한다.
2. 지역 인식 스타일에서 더 최적화된 가장 단단한 픽셀을 재귀적으로 선택하여 패치별 기능 수준 선택 전략을 위한 세분화된 보완 역할을 하는 새로운 PRA Loss를 제안한다.
3. 우리는 4개의 데이터 세트에 대해 광범위한 실험을 수행하여 최첨단 경쟁자에 대한 방법의 우수성을 입증한다.

2. Our Approach
그림 2와 같이 밀도 분기와 신뢰 분기의 두 가지 병렬 분기가 있습니다.
1) 밀도 분기 - 5개의 형상 수준을 사용하여 밀도 맵을 예측
2) 신뢰 분기 - 특정 이미지 패치에 가장 적합한 Feature level을 나타내기 위해 신뢰 점수를 예측
적응형 선택 전략을 사용하여 최종 예측 밀도 맵을 얻은 후 PRA Loss에 의해 밀도 맵에서 지역 인식 하드 픽셀(region-aware hard pixels)을 추가로 선택하고 세분화된 방식(fine-grained way)으로 최적화한다.
2-1. Scale Adaptive Selection
위 그림 에 표시된 것처럼 다중 스케일 특징 표현(Feature Representation)은 백본 네트워크에서 서로 다른 수준의 특징을 사용하여 계층적으로 생성된 {P1;P2;P3;P4;P5}로 표시된다. 그러나 특정 Pi에 대한 수용 필드(receptive field)가 제한되어 있기 때문에 좁은 범위의 스케일 내에서 헤드를 예측하는 데만 적합하다.
다중 스케일 기능 표현을 최대한 활용하기 위해 먼저 밀도 분기와 함께 스케일에 구애받지 않는 방식으로 Pi를 사용하여 독립적으로 예측한다. 그런 다음 신뢰 분기의 도움을 받는 가장 적절한 Feature level에서 예측을 선택하여 최종 예측을 얻는다. 특정 패치의 헤드가 대략 동일한 척도를 공유한다는 관찰을 통해 이러한 선택 전략은 패치별 스타일로 수행됩니다. 그리고 각 패치에 대해 선택된 기능 수준은 해당 예측에 대한 더 낮은 계수 오류를 달성할 수 있는 것으로 간주된다.
2-2. 밀도 분기(브랜치)
위 그림과 같이 밀도 분기는 각각 {P1;P2;P3;P4;P5}을 이용한 예측을 담당하는 5개의 밀도 헤드로 구성된다. 각 밀도 헤드에서 고품질 밀도 맵을 얻기 위해 다중 분기 모듈(multi-branch module)을 사용하여 여러 세분화된 스케일에 걸쳐 컨텍스트 정보를 집계한다. 모듈은 3개의 컨볼루션 분기와 1개의 스킵 연결 분기로 구성됩니다. 컨볼루션 분기의 경우 먼저 채널 감소를 위해 1 x 1 컨볼루션을 사용한 다음 커널 크기가 다른 컨볼루션을 채택하여 다양한 수용 필드에서 컨텍스트 정보를 획득한다. 다중 분기 모듈에서 출력되는 특징(feature)은 채널 차원을 따라 연결된 후 1 x 1 컨볼루션을 사용하여 i번째 특징 수준(feature level)에 대한 예측을 얻는다. 마지막으로, 우리는 각 피처 레벨의 예측 밀도 맵을 원래 입력과 크기가 같은 Di로 업샘플링한다. 이 밀도 헤드들은 동일한 지상 실측 밀도 맵 Dgt로 Supervised된다. 그리고 우리는 예측된 밀도 맵 Di와 Dgt 사이의 유클리드 거리를 손실 함수로 사용한다. 그런 다음, 다른 수준의 손실은 밀도 분기 손실 Lden으로 합계되며, 이는 다음과 같이 정의됩니다:


2-3. Confidence 브랜치.
예측된 밀도 맵 {D1;D2;D3;D4;D5}을 획득한 후, 우리는 다중 스케일 피쳐 표현을 최대한 활용하기 위해 특정 패치에 대한 최소 계수 오류가 있는 예측을 선택하려고 한다. 그러나 추론 중에 실측 자료에 액세스할 수 없기 때문에 최소 계수 오류로 가장 적절한 특징 수준을 결정하는 것은 불가능하다. 따라서, 우리는 각 피쳐 레벨에 대해 하나씩 5개의 신뢰 헤드를 포함하는 기능 수준 선택을 지원하는 신뢰 분기를 제안한다. 신뢰 헤드는 특정 패치에 가장 적합한 피쳐 수준이라는 신뢰를 나타내기 위해 점수를 예측합니다.
우리는 피쳐 {P1;P2;P3;P3;P4;P5}을 사용하여 신뢰 헤드와 함께 생성되는 신뢰 맵을 {C1;C2;C3;C4;C5}로 나타낸다. 구체적으로 패치별 선택을 수행하기 때문에 먼저 Pi를 원래 입력 이미지의 1/k 크기로 다운샘플링한다. 그런 다음 다운샘플링된 특징은 두 개의 3x3 컨볼루션으로 처리되며, 이는 Sigmoid 함수에 의해 변조되어 신뢰도 맵 Ci를 얻는다. 신뢰도 맵 Ci의 점수 값은 i번째 피쳐레벨이 특정 k x k 패치를 예측하는 데 가장 적합한 수준이라는 신뢰도를 나타낸다. 신뢰 맵 Ci에 대한 GT 레이블(그림2의 맨 우측)은 예측된 밀도 맵 Di와 지상 진실 Dgt의 비교에 의해 생성된다. 우리는 그림 2에서 단순성의 예로 5개의 피쳐 레벨 중 3개를 선택하는 프로세스를 설명한다.
먼저, 우리는 각각의 예측 밀도 맵 Di를 중복되지 않고 k x k 크기의 여러 패치로 나눈다. 그런 다음 모든 패치의 크라우드 수를 나타내는 카운팅 맵 Mi를 얻으며, 크라우드 수는 각 패치 내부의 밀도 값의 합계이다. 마찬가지로, 우리는 실측값 Dgt에 대한 계수 맵 Mgt를 가지고 있다. 마지막으로, 신뢰도 맵 Ci의 실측값 레이블은 다음과 같이 생성된다.

여기서 Cgt는 (m; n)에 위치한 패치의 i번째 피쳐레벨의 실측값 레이블을 나타내며, Mi은 i번째 피쳐 레벨의 예측 군집 수를 나타내며, Mgt는 패치의 실측값 군집 수를 나타낸다. 결과적으로 Cgt에 대한 양의 레이블은 i번째 피쳐 수준이 (m, n)에 위치한 패치의 예측에 가장 적합한 수준임을 나타냅니다. 음수 레이블은 i번째 피쳐 수준이 가장 부적절하다는 것을 나타냅니다. 레이블이 -1인 패치는 교육 단계에서 무시됩니다.
신뢰 헤드는 이진 교차 엔트로피(BCE) 손실로 감독된다. D 여기서 Ki는 i번째 수준에서 신뢰 레이블이 0 또는 1인 패치 집합, jKij는 Ki의 패치 수, Lce는 BCE 손실, Lconf는 신뢰 분기의 총 손실을 나타낸다.

2-4. 선택 전략.
훈련 중 가장 적합한 기능 수준은 계수 오차가 최소인 기능 수준으로 간주된다. 추론 중에 신뢰 분기의 도움을 받아 가장 적절한 특징 수준이 신뢰 점수로 표시된다. (m;n)에 위치한 패치의 경우, 최대 신뢰도 점수를 가진 기능 수준 j를 가장 적절한 기능 수준으로 선택한다. 즉, j = B. 그러나 헤드의 스케일 분포는 연속적인 반면, 다단계 네트워크의 다중 스케일 기능은 이산적이다. 결과적으로, 추론 중에, j번째 특징 수준의 밀도 맵에서 해당 영역을 (m; n)의 패치에 대한 예측으로 직접 사용하는 것은 차선이다. 대신, 우리는 또한 가중 평균을 통해 다른 특징 수준의 예측을 고려하는데, 이는 이산 특징 수준과 연속적인 규모 변동 사이의 격차를 완화하는 데 도움이 된다. 구체적으로, 그림 2에 나와 있는 것처럼, 우리는 먼저 연결을 통해 신뢰 맵 {C1;C2;C3;C4;C5}을 집계하고 Softmax 함수를 사용하여 5가지 기능 수준에 걸쳐 정규화한다. 그런 다음 Ci의 정규화된 신뢰 맵은 Di와 동일한 크기의 C0i에 가장 가까운 보간을 사용하여 크기가 조정됩니다. 마지막으로, 우리는 예측 밀도 맵 {D1;D2;D3;D4;D5}에 가중 평균을 적용하기 위해 C'i를 가중치 계수로 사용한다. 따라서 최종 예측 밀도 맵의 픽셀(j, k)에 대해, 우리는 아래를 가진다.
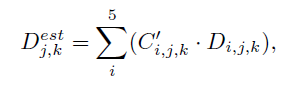
여기서 Dest_j,k는 최종 추정 밀도 맵의 픽셀(j, k)에 대한 밀도 값을 나타낸다.

2-5. 피라미드 지역에 대한 인식 상실
PRA 손실은 패치 내에서 가장 hard한 픽셀에 대해 세밀한 최적화를 수행하도록 설계되었다. 적응형 선택 전략은 패치별 스타일로 최종 예측에 가장 적합한 피처레벨을 선택한다. 그러나 패치 내의 픽셀은 다양한 학습 난이도를 가지며 서로 다른 계수(counting) 오류를 일으킨다. 특히 과대 추정된 패치에서 추정된 군중 수가 실제보다 큰 과대 추정된 픽셀은 최대 계수 오류에 기여하며, 그 반대의 경우도 마찬가지이다. 따라서 이러한 가장 hard한 픽셀에 대한 최적화에 더 주의를 기울인다면 전체 계수 오류가 더 줄어들 수 있다.
좀 더 구체적으로 말하자면, 과대평가(예측값이 실제보다 매우 큰)된 지역을 예로 들면, 과대평가된 지역을 4개의 더 작은 하위지역으로 균등하게 나눈다면, 과대평가된 하위지역은 적어도 하나는 있어야 한다. 이러한 과대평가된 하위 영역은 전반적인 과대평가 문제에 큰 기여를 하기 때문에 더욱 최적화되어야 한다. 반대로 과소 추정된 하위 영역은 상위 영역의 과대 추정 문제를 어느 정도 완화하는 데 도움이 되므로 PRA 손실에서 무시되고 정상 영역으로만 최적화된다. 우리는 가장 hard한 픽셀의 검색 프로세스로 PRA 손실에 대한 소개를 시작한다.
그림 4(a)에 나타난 바와 같이, 우리는 영역 레벨(전체 이미지)에서 픽셀 레벨까지 재귀 검색 프로세스를 수행한다. 과도하게 추정된 특정 영역에 대해, 우리는 먼저 그것을 4개의 하위 영역으로 나눈다. 그리고 이 하위 지역의 군중 수를 계산합니다. 그런 다음, 실제값과 비교하여, 우리는 그들로부터 지나치게 추정된 하위 영역을 선택할 수 있다. 이렇게 선택된 하위 영역은 다시 검색 알고리즘에 입력되고, 이 과정은 픽셀 레벨에 도달할 때까지 반복됩니다. 최종 선택된 픽셀은 전체 이미지에서 가장 Hard한 픽셀로 간주되며 PRA 손실로 더욱 최적화됩니다.
검색 프로세스의 시각화는 그림 4(b)에 나와 있습니다. 선택된 가장 단단한 픽셀은 가중 유클리드 거리 손실에 의해 더욱 최적화된다. 따라서 최종 PRA 손실은 다음과 같이 정의됩니다.
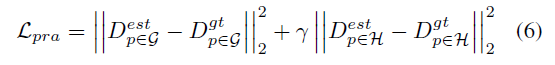
여기서, p는 최종 예측 밀도 맵(Dest, G 및 H)에서 픽셀을 나타내며, Dest 내의 모든 픽셀의 집합과 가장 Hard한 픽셀의 집합을 각각 나타내며, 하드 픽셀에 대한 가중치 용어이다. PRA 손실은 또한 훈련 목표와 평가 지표 사이의 불일치를 줄이는 데 도움이 된다는 것을 언급할 가치가 있다. 훈련 중에 널리 채택된 훈련 손실은 정확한 픽셀 단위 회귀를 강조하는 반면, 평가 메트릭은 지역의 군중 수에만 초점을 맞춘다. 따라서 훈련 손실이 최소인 수렴 모델은 테스트 시 최적의 계수 정확도를 보장할 수 없다. 가장 단단한 픽셀은 상위 영역이 과대평가되었는지 과소평가되었는지에 대한 인식으로 선택되기 때문이다. 픽셀과 영역 간의 이러한 포함 관계를 고려한 후 PRA 손실은 위의 불일치를 줄이는 데 도움이 된다.
2-6. 모델 학습
최종 훈련 손실 Lfinal은 위의 세 가지 손실, 즉 Lden, Lconf 및 Lpra의 합계이다. 보다 공식적으로, Lfinal은 다음과 같이 정
의된다.
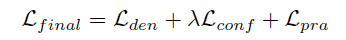
여기서 sigma는 Lconf의 효과의 균형을 맞추기 위한 중량항이다.
2-7. 백본 네트워크
그림 2에 나와 있는 것처럼, 우리는 VGG-160_bn의 첫 13개 컨볼루션 레이어를 인코더 네트워크로 사용한다. 구체적으로 다운샘플링 단계가 각각 {1, 2, 4, 8, 16}인 총 5개의 피쳐레벨이 있으며, 해당 피쳐맵은 {V1; V2; V3; V4; V5}로 표시된다. 각 디코딩 단계에서의 특징 맵 Pi는 다음과 같이 Vi와 Pi+1의 조합에 의해 생성된다.
첫째, 더 높은 수준의 피처 맵 Pi+1은 Vi와 동일한 크기로 가장 가까운 이웃 보간법을 사용하여 업샘플링된다.
그런 다음 업샘플링된 맵이 채널별 연결에 의해 Vi와 결합됩니다. 마지막으로, 우리는 ReLU 활성화가 있는 3 x 3 컨볼루션을 병합된 맵에 추가하여 최종 피처 맵 Pi를 생성한다. 특히, P5는 V5에 콘볼루션을 적용하는 것만으로 생성된다.
3. 실험
우리의 백본 인코더는 ImageNet에서 사전 훈련된 VGG-160_bn의 첫 번째 13개 컨볼루션 레이어로 구성된다. 훈련하는 동안, 우리는 각 시대에 대해 8개의 이미지를 무작위로 선택하고 각 이미지에서 128 x 128의 고정 크기로 4개의 이미지 패치를 자른다. 따라서 유효 배치 크기는 32입니다.우리는 또한 데이터 증강으로 확률이 0.5인 무작위 수평 플립을 사용한다. 신뢰 분기의 이미지 패치 크기 k는 32로 설정됩니다. 무게 항은 1로 설정되고 S는 10으로 설정됩니다. 우리는 1e-5의 고정 학습률로 Adam 알고리듬(Kingma 및 Ba 2014)을 사용하여 모델을 최적화한다.
즉, 그림2로 판단을 하면
1) 우선 VGG16을 진행하면서 피쳐맵 V1~V5를 만든다. [2-7과정]
이렇게 만든놈들은 디코딩 작업을 거친다. 이 때 P1은 V1과 P2로 만들어지고, P2는 V2와 P3으로 만들어진다.
디코더 블록을 보면 알 수 있는데, P4의 경우 VGG16을 통과한 16배로 다운샘플링 된 피처맵 P5가 V4사이즈로 업샘플링 되면, 이를 V4와 Channel Concatenation(채널별 연결, 결합) 후 ReLU 활성화함수가 있는 3x3 컨볼루션을 진행하여 P4를 생성한다. 이를 반복해 P1을 만듦.
2) 이렇게 각각 생성된 P1~P5는 일종의 '다분화된 스케일'임. 이 여러 스케일들을 각자 Confidence Head와 Density Head를 통과함. 그러면 우선
2-1) 채널 감소를 위해 1x1 컨볼루션을 진행 후, 각자 Conv1, Conv3, Conv5 등 커널 크기가 다른 컨볼루션을 선택해, 다양한 수용필드에서 Context 정보를 획득한다. [2-2 과정] 이는 일종의 i번째 특징수준의 예측을 획득하는 것이다(이때 i = 1~5). 다음으론 Channel Concatation을 진행한 다음 Conv1을 통해 3개로 나눠진 것들을 하나로 합쳐 하나의 Denstity map을 획득한다. 이는 '밀도분기'로, Conv1와 Conv3, Conv5를 통해 1, 3, 5 픽셀 주위의 context를 획득하여 주위의 밀도상황 판단이 가능해진다. 이 밀도맵은 원래 입력과 크기가 같도록 다시 업샘플링된다.
2-2) 위 과정을 통해 얻은 밀도맵 D1~D5에서, 저자는 다중 스케일 피쳐 표현을 최대한 활용하기 위해 특정 패치에 대한 최소 계수 오류가 있는 예측을 선택하고 싶어 한다. 이게 뭔소리냐? 여러 밀도맵을 만들었으니 이것들을 잘 버무려서 최대한 GT와 가까운 값을 만들겠단 거다. 그림을 보면 알 수 있는데, 우선 Pi를 1/k로 다운샘플링 한 후, 2번의 3x3 컨볼루션 + Sigmoid을 진행한다. 이렇게 되면 Ci가 만들어지는데, Ci의 점수값은 'i번째 피쳐레벨이 kxk 패치를 예측하는 신뢰도 값'이라는 뜻이라고 한다. 이게 뭔소리냐?
Sigmoid를 진행했으니 0~1의 값이 나올 거다. 그리고 Ci에 대한 gt는 그림 2처럼, 각 1~5의 패치의 밀도값중 실제 GT와 가장 가까운 패치는 1, 가장 멀면 -1의 값을 갖게 되는 것을 볼 수 있음. 따라서 3x3으로 나눴으면 각 구역당 1이 4개, -1이 4개, 나머지는 0이겠지? [2-3]의 마지막 식을 통해 손실함수를 계산해가면서, 그리고 예측값 Di와 그 GT인 Dgt 등등을 계산해가면서 '2번의 3x3 컨볼루션 및 Sigmoid'는 최종적으로 각 1~5개의 Map중 몇 번째 Map의 어떤 구역이 가장 신뢰할만한지에 대한 정보를 획득하게 된다.
예를 들어 (m,n)에 위치한 패치들중 최대 신뢰도점수를 가진 Feature level이 가장 적절한 것으로 선정된다.
3) 이제 이렇게 Confidence Map과 Density Map을 얻었다. '가장 적절한 Feature level'이 신뢰점수로 표시되었다. 그러나 이산적 Feature level과 연속적인 Scale변동 사이에는 차이가 있다(이는 이전에 앞서 말한 여러 논문에서도 지적하는 바). 헤드의 스케일분포는 연속적이지만 다단계 네트워크의 다중스케일 Feature은 이산적이다. 이를 완화하기 위해, 즉 0~1 분포로 만들기 위해 C1~C5에 대해 Softmax를 진행한다. [2-4 과정]
이젠 Di를 각자 자기 쌍에 맞는 Ci과 사이즈를 동일하게 하기 위해 보간으로 크기를 조정한 후, Di에 가중평균을 적용한다. 이는 다른 feature level의 예측을 고려하여 이산 기능 수준과 지속적인 스케일 변동 간의 격차를 완화하는 효과를 지닌다고 한다. 그렇다면 그런거겠지 뭐, 나도 원리는 몰라! 아무튼 이렇게 하면 최종적으로 Dest_j,k는 최종 추정 밀도 맵의 픽셀(j, k)에 대한 밀도 값을 갖는다고 한다!
아무튼 이렇게 해서 다 곱하고 더하면 결과가 나온다. Density Map는 말 그대로 context를 배우는 거고, confidence map은 각 P에 대해 '사람 예측 수'를 배워, 둘을 Dot하고 각 1~5를 더하여 최종 결과를 낸다고 한다.
4) 마지막으로 [2-5 과정]이다.
이는 Pyramid Region Awareness Loss, 즉 PRA손실 계산 과정이다. 이건 걍 어떤 구역 중 가장 크게 나온 놈이 있으면, 이걸 나눠서 그중 가장 크게 나온거에 기여한 놈을 줄여가는 재귀적 과정이다.
'버츄얼유튜버' 카테고리의 다른 글
| NVIDIA-SMI 및 기타 환경 구축 (0) | 2022.12.06 |
|---|---|
| Tracking Pedestrian Heads in Dense Crowd (0) | 2022.12.04 |
| Generating High-Quality Crowd Density Maps using Contextual Pyramid CNNs (0) | 2022.12.02 |
| Density Map 작성법 (0) | 2022.11.29 |
| DataLoader 이해 - Boosting-Crowd-Counting... 을 기반으로 (0) | 2022.11.29 |


