
1. **두 개의 네트워크**: BYOL은 두 개의 신경망을 사용한다:
- **온라인 네트워크**: 주 학습자입니다.
- **대상 네트워크**: 온라인 네트워크의 복사본이지만 특별한 방법으로 업데이트됩니다.
2. **Data Augmentation**: 데이터 세트의 각 이미지에 대해 두 개의 서로 다른 증강 뷰를 만듭니다. 이들은 원본 이미지의 약간 회전, 잘라내기, 색상 조정 버전을 만들 수 있습니다.
3. **전달 패스**:
- 하나의 증강 뷰를 온라인 네트워크를 통해 전달한 다음 예측 변수를 통해 표현을 얻습니다.
- 다른 표현을 얻기 위해 다른 증강 뷰를 대상 네트워크에 전달합니다.
4. **손실 계산**: 목표는 온라인 네트워크 + 예측기로부터의 표현을 대상 네트워크로부터의 표현과 유사하게 만드는 것이고, 그 반대도 마찬가지이다. 이는 코사인 유사도와 같은 유사도 측정치를 사용하여 수행된다.
5. **역방향 전파**: 손실의 그레이디언트를 사용하여 온라인 네트워크(및 해당 예측 변수)를 업데이트합니다. 대상 네트워크는 역방향 전파를 사용하여 업데이트되지 않습니다.
6. **타겟 네트워크 업데이트**: 역방향 전파 대신, 타겟 네트워크는 온라인 네트워크로부터 가중치를 천천히 복사함으로써 업데이트된다. 이것은 지수 이동 평균(EMA)을 사용하여 수행된다. 이것은 타겟 네트워크가 항상 온라인 네트워크보다 뒤쳐지고, 더 느리게 변화한다는 것을 의미한다.
7. **반복**: 각 데이터 배치에 대해 2-6단계를 반복합니다.
BYOL의 핵심 아이디어는 대조 학습을 위해 부정적인 샘플(dissimilar 쌍)이 필요하지 않다는 것이다. 대신, 당신은 같은 이미지의 두 개의 증강 뷰를 사용하고 그들의 표현을 유사하게 만들려고 한다. 천천히 업데이트되는 타겟 네트워크는 움직이는 타겟으로 작용하여 일관성의 형태를 제공하고 모델이 사소한 해결책(trivial solution)을 학습하는 것을 막는다.
본질적으로 BYOL은 부정적인 예를 명시적으로 사용하지 않고 온라인 네트워크가 동일한 이미지의 서로 다른 관점을 유사한 것으로 인식하도록 가르치고 있다. 타겟 네트워크는 학습 측면에서 항상 온라인 네트워크보다 약간 뒤떨어지는 기준점의 역할을 한다.
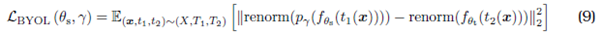
데이터셋 X로부터 샘플 x 획득, 또한 변환함수 T1과 T2가 존재.
각각 온라인/타겟 네트워크로부터 나온 feature임. 즉, f(t1(x))는 온라인/타겟 네트워크로부터 나온 x의 transform 1, 2 이미지의 feature.
pr은 온라인 네트워크의 출력을 타겟 네트워크의 공간에 매핑하는 predictor function.
다음으로 이것들의 거리를 잼(renorm). 이 거리의 최소화가 곧 목표.
1) Photometric loss
The equation you've provided seems to be a loss function \( L(D, \theta) \) for some model or algorithm. Let's break it down in simpler terms:
\[ L(D, \theta) = \omega_{photo}L_{photo}(D, \theta) + \omega_{smooth}L_{smooth}(D, \theta) + \omega_{self}L_{self}(D, \theta) \]
Here's what each term means:
1. **\( L(D, \theta) \)**: This is the total loss that the model wants to minimize. It's a measure of how well the model is doing. The lower the loss, the better the model's predictions are.
2. **\( \omega_{photo}L_{photo}(D, \theta) \)**: This term represents the photometric loss. The photometric loss measures how well the model's predictions match the actual images. The \( \omega_{photo} \) is a weight that determines how important this loss is compared to the others.
3. **\( \omega_{smooth}L_{smooth}(D, \theta) \)**: This term is the smoothness loss. It ensures that the model's predictions are smooth and don't have abrupt changes. The \( \omega_{smooth} \) is a weight for this loss.
4. **\( \omega_{self}L_{self}(D, \theta) \)**: This term is the self-supervision loss. Self-supervision is a way to train models without labeled data. The model generates its own labels and then tries to match its predictions to these self-generated labels. The \( \omega_{self} \) is a weight for this loss.
In simpler terms, the equation is saying: "The total error (or loss) of our model is a combination of how well it matches the images, how smooth its predictions are, and how well it does on its self-generated tasks. The \( \omega \) values determine the importance of each of these losses."
+++++++++++
Photometric loss, often used in computer vision tasks, especially in optical flow and depth estimation, measures the consistency between pixel intensities (or colors) of two images after one has been warped or transformed to align with the other.
Let's break it down with a simple analogy:
Imagine you have two photos: one is the original, and the other is a slightly shifted or transformed version of the first. If you overlay the transformed photo on top of the original, some parts will align perfectly, while others might not.
**Photometric loss** is like a tool that checks how well the colors of the overlaid parts match. If the colors match perfectly everywhere, the loss is zero (or very low). If they don't match in many places, the loss is high.
In technical terms, for each pixel in the transformed image, the photometric loss computes the difference in intensity (or color) between that pixel and the corresponding pixel in the original image. The goal during training is to minimize this difference, ensuring that the transformation is as accurate as possible.
In many applications, using photometric loss is beneficial because it doesn't require labeled data. Instead, it leverages the inherent consistency in the data itself to guide the learning process.
+++++++++++
Alright, let's break down the equation for the photometric consistency term, \( L_{photo}(D, \theta) \):
\[ L_{photo}(D, \theta) = \frac{1}{HW} \sum O_1 \odot \rho(I_1, w(I_2, V_1)) \]
Here's what each component means:
1. **\( L_{photo}(D, \theta) \)**: This is the photometric loss we're trying to compute. It measures how consistent two images are in terms of their pixel intensities after one has been transformed or warped.
2. **\( \frac{1}{HW} \)**: This is an averaging term. \( H \) and \( W \) represent the height and width of the images, respectively. By dividing by this, we're taking an average over all the pixels in the image.
3. **\( \sum \)**: This represents a summation. We're summing up the values for all pixels in the image.
4. **\( O_1 \)**: This is likely a mask or an occlusion term. In the context of warping images, some parts of the image might not have corresponding parts in the other image (e.g., if they're out of frame). This term ensures we only consider pixels that are visible in both images.
5. **\( \odot \)**: This is the Hadamard (element-wise) product. It multiplies two matrices (or images) element by element.
6. **\( \rho(I_1, w(I_2, V_1)) \)**: This is the core of the photometric consistency term. Here:
- \( \rho \) is a function that measures the difference between two images. Common choices are the absolute difference or squared difference between pixel intensities.
- \( I_1 \) is the first image.
- \( w(I_2, V_1) \) represents the warping of the second image \( I_2 \) using a flow or transformation \( V_1 \). This warping function aligns \( I_2 \) to \( I_1 \) based on the estimated motion or transformation.
In simpler terms, the equation calculates the average difference between the pixels of the first image and the warped version of the second image, but only for pixels that are visible in both images (as indicated by \( O_1 \)). The goal is to minimize this difference, ensuring that the warping or transformation is accurate.
+++++++++++
The statement you provided describes a specific method to measure the photometric difference between two images. Let's break it down:
1. **ρ(·, ·)**: This function measures the photometric difference between two images. Photometric difference essentially quantifies how different two images are in terms of their pixel intensities.
2. **Soft Hamming distance on the Census-transformed images**:
- The **Census transform** is a non-parametric local image operator that provides a binary representation of an image region. It compares the intensity of a pixel to its neighbors and produces a binary string (or number).
- The **Soft Hamming distance** is a measure of the difference between two binary strings. In the context of images, it would measure the difference between the Census-transformed representations of two image regions. The "soft" part indicates that it might not be a strict 0 or 1 difference count but could involve some form of weighting or soft comparison.
3. **Generalized Charbonnier function**: This is a robust error function used in optimization problems, especially in image processing. It's less sensitive to outliers than the squared error. The Charbonnier function is defined as:
\[ \rho(x) = \sqrt{x^2 + \epsilon^2} \]
where \( \epsilon \) is a small constant to ensure stability. The "generalized" part might indicate some modifications or extensions to the basic Charbonnier function.
In simpler terms, the function \( \rho(·, ·) \) calculates the difference between two images by first transforming them into a binary representation using the Census transform. It then measures the difference between these binary representations using a Soft Hamming distance. Finally, this difference is passed through the generalized Charbonnier function to get a robust measure of the photometric difference between the two images.
+++++++++++
Certainly! Let's break this down with a simple analogy:
Imagine you have two photographs of a flying kite taken a few seconds apart. In the first photo (let's call it \( I_1 \)), the kite is on the left side of the sky. In the second photo (let's call it \( I_2 \)), the kite has moved to the right due to the wind.
Now, if you wanted to align or "match" the position of the kite in \( I_2 \) to its position in \( I_1 \), you would need to "shift" or "move" the kite in \( I_2 \) to the left. This process of shifting or moving is called "warping."
Here's what the terms in the statement mean:
1. **w(I2, V1)**: This is the warping function. It takes the second image \( I_2 \) and a "flow" or "transformation" \( V_1 \) as inputs.
2. **I2**: This is the second image (like the photo of the kite on the right side of the sky).
3. **V1**: This represents the estimated motion or transformation needed to align \( I_2 \) with \( I_1 \). In our kite analogy, \( V_1 \) would describe how much and in which direction we need to move the kite in \( I_2 \) to match its position in \( I_1 \).
4. **Warping**: This is the process of transforming or adjusting an image based on a specific motion or transformation. In the context of images, warping can involve shifting, rotating, scaling, or any combination of these to align one image with another.
In essence, the statement describes a process where the second image \( I_2 \) is adjusted or "warped" based on the estimated motion \( V_1 \) to align it with the first image \( I_1 \). This is useful in many computer vision tasks, such as optical flow estimation, where the goal is to understand the motion between consecutive frames in a video.
features[version] =
{'correlation_pyarmid_fw':
[<tf.Tensor 'raft_feature_siamese/Reshape_4:0' shape(3219, 37, 87, 1) dtype=float32>,
<tf.Tensor 'raft_feature_siamese/AvgPool:0' shape=(3219, 18, 43, 1) dtype=float32>,
<tf.Tensor 'raft_feature_siamese/AvgPool_1:0' shape=(3219, 9, 21, 1) dtype=float32>,
<tf.Tensor 'raft_feature_siamese/AvgPool_2:0' shape=(3219, 4, 10, 1) dtype=float32>],
'net_1': <tf.Tensor 'raft_feature_siamese/Tanh:0' shape=(1, 37, 87, 128) dtype=float32>,
'inp_1': <tf.Tensor 'raft_feature_siamese/Relu:0' shape=(1, 37, 87, 128) dtype=float32>,
'original_size': (<tf.Tensor 'raft_feature_siamese/strided_slice_1:0' shape=() dtype=int32>,
<tf.Tensor 'raft_feature_siamese/strided_slice_2:0' shape=() dtype=int32>),
'batch_size': <tf.Tensor 'raft_feature_siamese/strided_slice:0' shape=() dtype=int32>,
'correlation_pyarmid_bw': [<tf.Tensor 'raft_feature_siamese/Reshape_3:0' shape=(3219, 37, 87, 1) dtype=float32>,
<tf.Tensor 'raft_feature_siamese/AvgPool_3:0' shape=(3219, 18, 43, 1) dtype=float32>,
<tf.Tensor 'raft_feature_siamese/AvgPool_4:0' shape=(3219, 9, 21, 1) dtype=float32>,
<tf.Tensor 'raft_feature_siamese/AvgPool_5:0' shape=(3219, 4, 10, 1) dtype=float32>],
'net_2': <tf.Tensor 'raft_feature_siamese/Tanh_1:0' shape=(1, 37, 87, 128) dtype=float32>,
'inp_2': <tf.Tensor 'raft_feature_siamese/Relu_1:0' shape=(1, 37, 87, 128) dtype=float32>}
SMURF
Lsmooth에선 k차 미분이 나오는데, 이미지에 k차미분을 하면 아래와 같은 효과를 획득.
영교차 이론 · Monch (songminkee.github.io)
영교차 이론 · Monch
코드링크 1980년도 이전에는 주로 소벨 마스크가 에지 연산자로 사용되었다. 그런 상황에서 1980년에 Marr와 Hildreth가 발표한 논문은 에지 검출에 새로운 물줄기를 만들었다. 가우시안과 다중 스케
songminkee.github.io

sigma을 조절해 일정 효과를 얻는다고 하는데, 일단 1.0일 때를 보면 edge를 기준으로 미분의 횟수가 많아질수록 더 색이 바뀌는 횟수가 증가하고 폭 역시 커지는 것을 볼 수 있음.
'성우리뷰' 카테고리의 다른 글
| [ConvLSTM] LSTM, RNN 확장판 (0) | 2023.04.28 |
|---|---|
| [프로그래머스] 소수찾기 lv2 (0) | 2023.04.14 |
| [프로그래머스] 큰 수 만들기 (0) | 2023.04.13 |
| (softeer) 로봇이 지나간 길 (0) | 2023.04.12 |
| [softeer] 업무처리 (0) | 2023.04.10 |
