[통계 정리] 확통 사이트 및 개념

8.6 다변수정규분포 — 데이터 사이언스 스쿨 (datascienceschool.net)

8.6 다변수정규분포 — 데이터 사이언스 스쿨

[머신러닝 순한맛] 다변량 정규분포(Multivariate Gaussian Distribution) in 이상 탐지(Anomaly Detection) (tistory.com)

[머신러닝 순한맛] 다변량 정규분포(Multivariate Gaussian Distribution) in 이상 탐지(Anomaly Detection)

이 때, |Σ| = (ad-bc)

평균만큼 빼줌으로써 0에 가까워지게 하고, 

그리고 그 모양은

이 때, 위의 식은

 

에 의존함을 주의. 즉, [2x2]라서 2*sqrt(5)가 된거다.

 

상관계수(correlation)

공분산에 각 확률변수의 분산을 나눠, 정규화시킨 것.

 

 

고윳값과 고유벡터 - 공돌이의 수학정리노트 (Angelo's Math Notes) (angeloyeo.github.io)

고윳값과 고유벡터 - 공돌이의 수학정리노트 (Angelo's Math Notes)

Ax = Sx(S는 스칼라) 일 때

x는 S의 고유벡터

S는 A의 고유값

 

마할라노비스 거리

즉, 보라색 경계선은 전부 가운데로부터 동점의 거리다.

마할라노비스 거리는 이를 정규화해준다.

기존 유클리드 거리(dE=√(→x−→y)(→x−→y)T)의 가운데에 공분산의 역행렬을 곱함으로써 계산이 가능.

 

잘 보면 알겠지만, 사실 저 뒤에 있는게 마할라노비스 거리임.

 

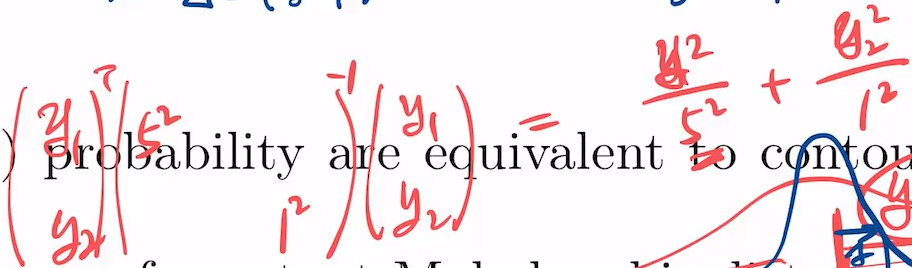
위와 같이 y1는 분산이 5고, y2는 1이라 하면, y1이 5까지의 값의 누적량 = y2이 1까지의 값의 누적량.

상대적으로 다른 값 가지는 걸 표준화 하는게 '표준화된 distance'이고 여기에 쓰는게 covariance. 

근데 이건 공분산의 xy가 0인 경우인데, 숫자가 있다면?

예를 들면

다음과 같은 x y 구하라 하면?

 

고윳값 분해(eigen-value decomposition) - 공돌이의 수학정리노트 (Angelo's Math Notes) (angeloyeo.github.io)

고윳값 분해(eigen-value decomposition) - 공돌이의 수학정리노트 (Angelo's Math Notes)

고유값분해는 돌리고, 늘리고 돌리기.

---

왼쪽은 아래와 식이 같음.

 

 

 

 

 

걍 식이 그렇다고 함.

그러면 이 공분산의 inverse는

 

 

 

왼쪽과 같이, scalar에 역수 취한 것임.

이것에 근거해 마할라노비스 거리를 다시 구하면

 

 

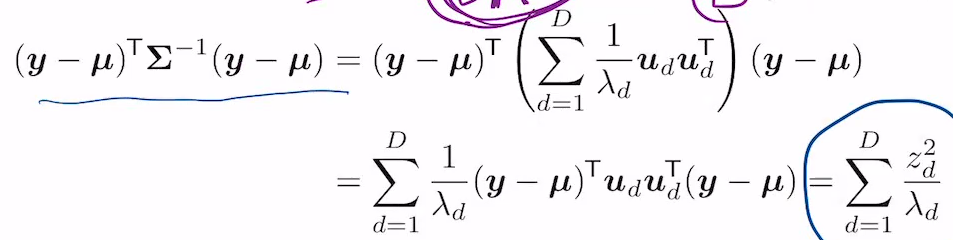
이렇게 나옴. 이 때 z는

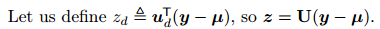
로 정의됨. 따라서, 2차원에서 가우시안은 타원형 모양이 되게 됨.

 

Marginal and conditions of an MVN

MVN 가정1

위와 같은 조건이 주어짐.

p(y1, y5)는 위의 5x5 sigma로부터 (1,5) (5,1) (5,5) (1,1)을 가져오면 됨.

 

conditonal covariance

y4, y5를 sample data로 받았을 때, 가정1을 알고 있어야 함. 아래와 같은 distribution을 구해야 함.

이 때 아래의 공식을 써야 함.

식 3.28

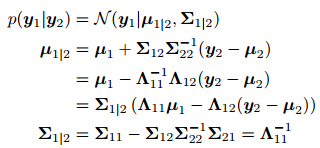
이는 7.109~7.114~7.118로 연결됨. 행렬이 diagonal이 되어가는 과정.

7.137은 7.118을 이용해 proof

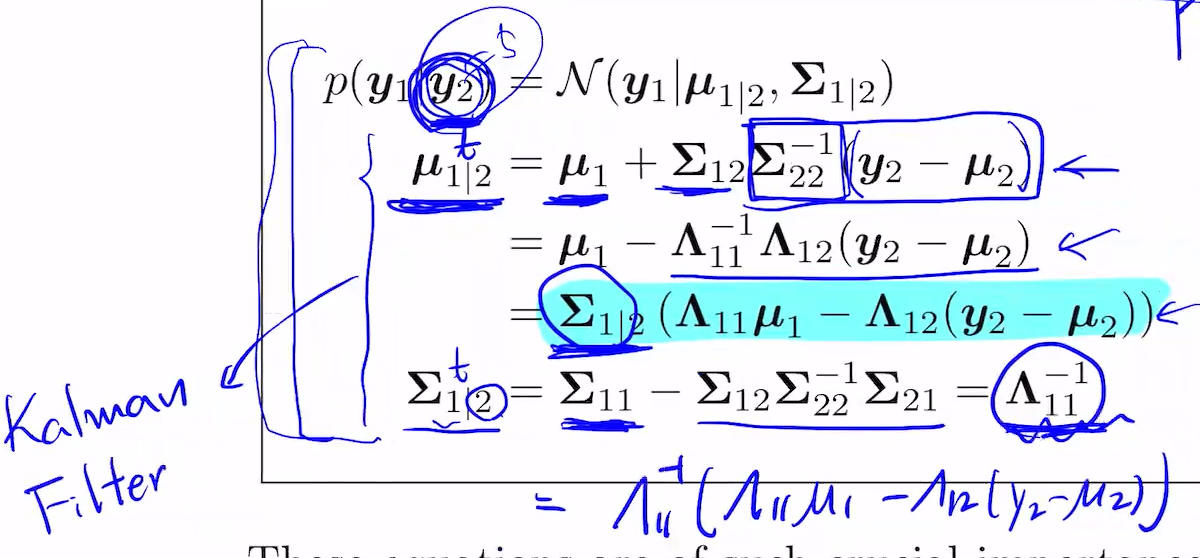
위의 y2를 t으로 적용한 연속된 것은 Kalman Filter가 됨.

 

만약 우리가 p(y0, ... yn)을 안다고 하자. 즉 Joint probability를 안다.

---

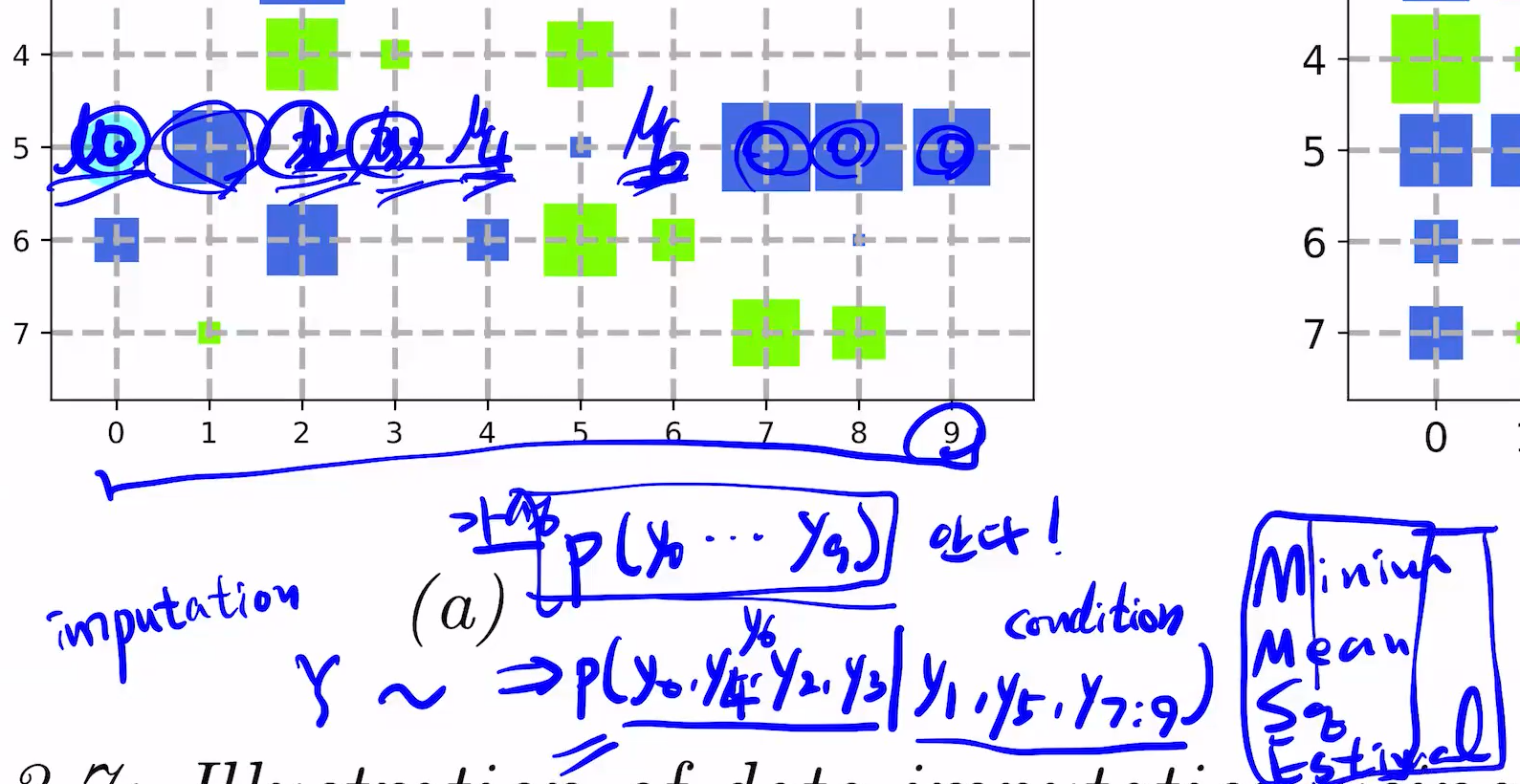
Linear Gaussain Systems

p(z,y) = ... 을 알면, p(z|y)를 구할 수 있을 것임.

3.26 폼으로 만들면, 이후 3.27, 3.28도 구할 수 있게 됨. 따라서

이 때 (I -W 0 I)는 앞의 과정을 통해 알게 됨.

그 앞의 (I 0 -Wt i)도, 그 앞의도.

Z와 Y의 Covariance inverse도 구하게 됨.

 

3.37과 3.38도 있다. 이거도 봐라.

베타-베르누이(앞이 prior, 뒤가 likelihood)는 beta가 나옴.

 

ML Estimate를 구하는 식(yi = 0.137일 때), NLL : Negative Log likelihood

SSE(Sum of Squared Estimation)을 구하는 방식. 이 때 Z=1/3 * (sigma yi)

 

그럼 bayesian으로 density는?

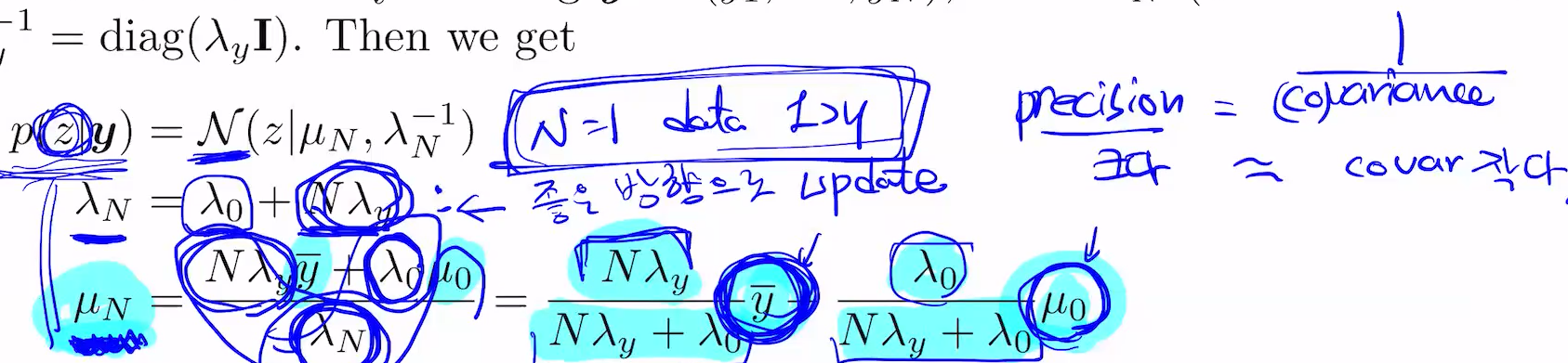
-y: 이게 가지는 precision

m0 : prior이 가지는 precision

이 두개로 weighted 되는 sum

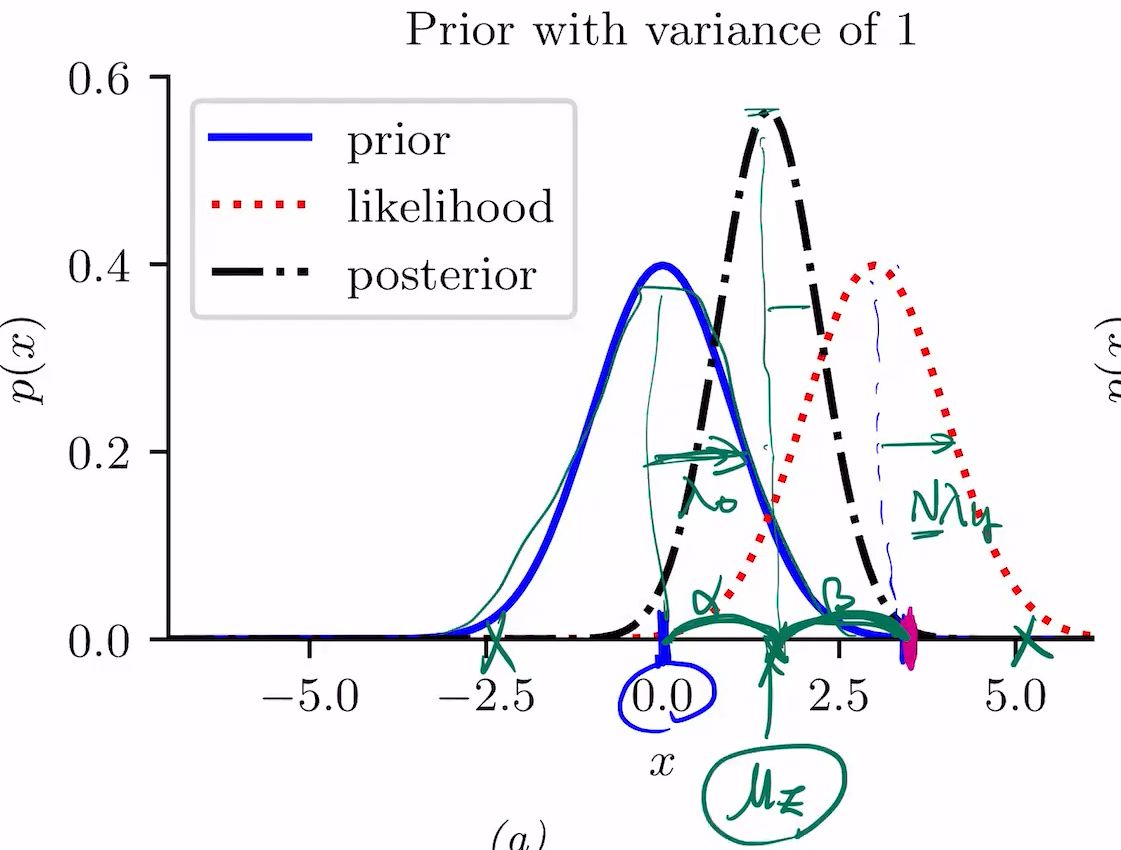
알파와 베타의 비율은 폭의 역수(precision) 람다제로, N(데이터수) * 람다와이로 결정.

이거로 weighted가 정해짐.

그 가운데에 Posterion의 mean이 존재

1 분산이므로 람다는 1

만약 4라면, 람다는 1/5=0.2

variance가 클 수록, 파란색은 flat에 가까워짐.

posterior가 prior의 값을 갖다 쓸 필요가 없어지니, likelihood는 점점 작아짐. likelihood와 posterior의 mean이 점점 가까워짐.

 

N=1일 때, prior의 precision + data의 precision은 람다1 = 람다0 + 람다y

그리고..

 

 

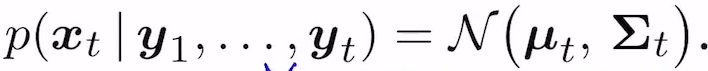
왼쪽이 주어졌다 하자. 그럴 때 

이것들을 구할 거임.

우선 1번.

COV의 왼쪽위는 xt+1의 variance, 아래오른쪽은 xt의 cov가 있을 예정.

LGS는 저 시퀀스를 따르면 됨.

 

p(xt+1)은 assume that.. 옆에 있고, p(yt+1|xt+1)은 2번문제에 올라가있다. 이를 적분한 것으로 나누면 conditional.

 

3.3.4 unknown vector inferring

z, yn ~ N(z, sigma y)일 때, (식3.65)에서 보면

 

x1 밑의 선은 x2=-1일 때. 여길 자르면 그 단면을 보여주는 것. scaling하는 이유는, 적분이 1이 되도록.

왼쪽의 0 2는 mean vector, cov vector은 각각의 분산. 이 값에 따라, 등고선이 좌대각/우대각이 될 수 있음. 이 행렬을 갖고 eigen decomposition을 해서 2개의 principal axis를 찾으면, principal axis vector은 magnitude가 1이 되어야 함. 그 2개가 나옴.

뮤1, 뮤2와 그에 대응되는 람다1, 람다2 나옴. 람다1이 람다2보다 크면, 타원이 더 긴쪽은 더 람다1(유1), 짧은쪽은 2.

precision matrix(회색칠한 둘째줄 맨 첫번째 구하는 식)

 

 

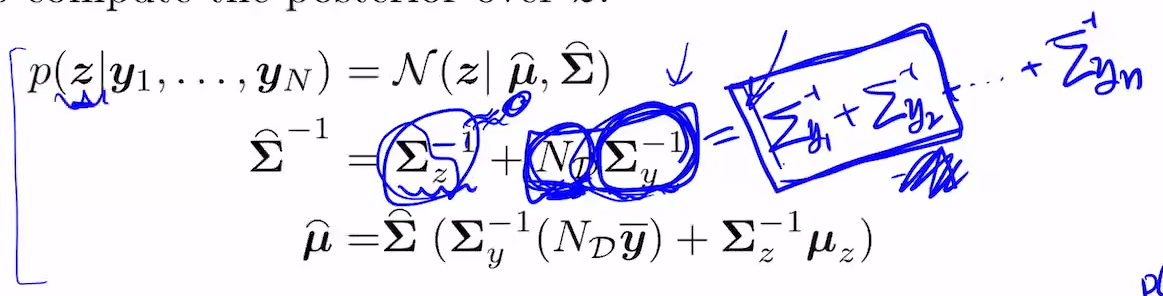
cov가 개크면 그 역수는 0에 가까워지고,

y1와 y2의 cov의 역수가 같으면, ND는 2이고,....

이게 어떤 영향을 끼치느냐.

몰라.

 

 

mixture component는 파이로 표현.

 

---

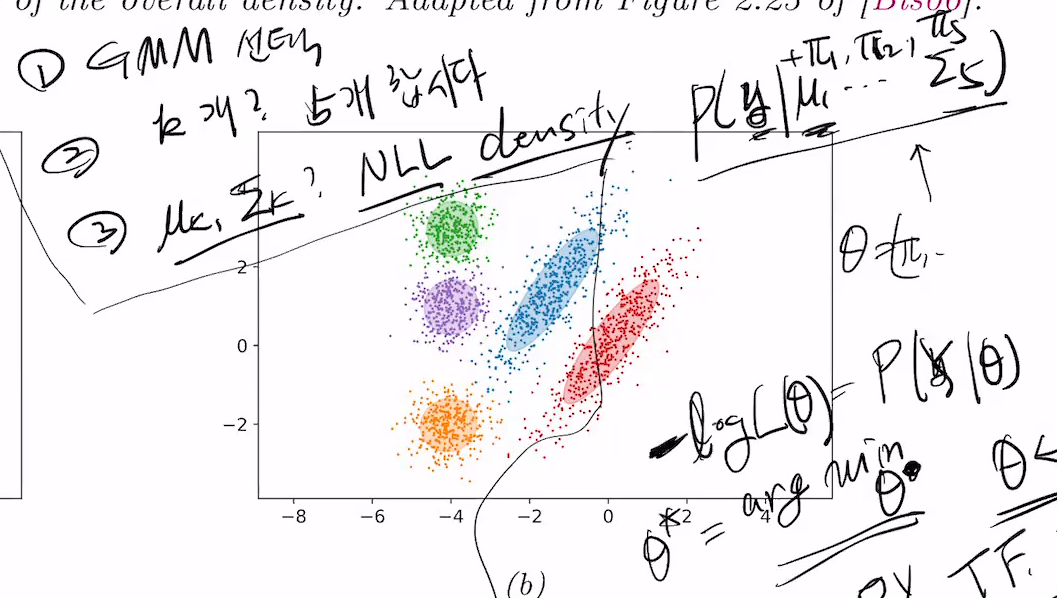
KL Divergence

2개의 확률분포가 얼마나 비슷할까? 2개에 대한 distnace를 구함.

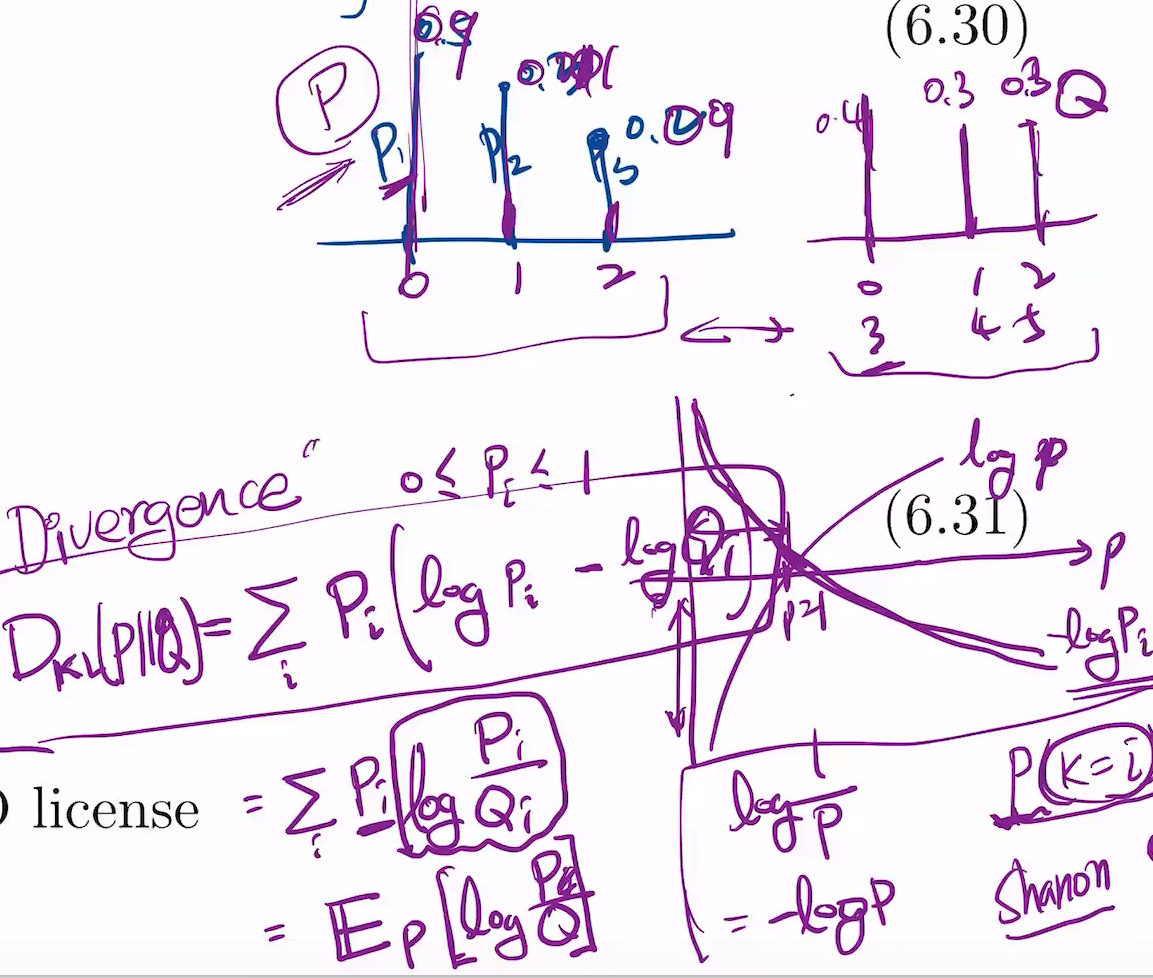
수학에서 distance는 일종의 metric

log를 취함으로써, 0~1을 무한으로 늘려버림.

어떤 probability는 0.9, 어떤건 0.001로 차이가 클 수 있음.

이 probability에 weight를 추가함. probability i(Pi)를 곱하고, 더함.

 

 

 

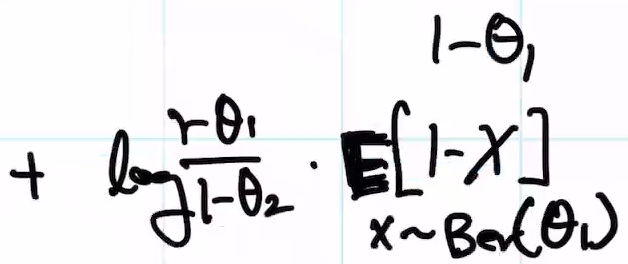
결론은, 

 

푸아송에서의 KL 

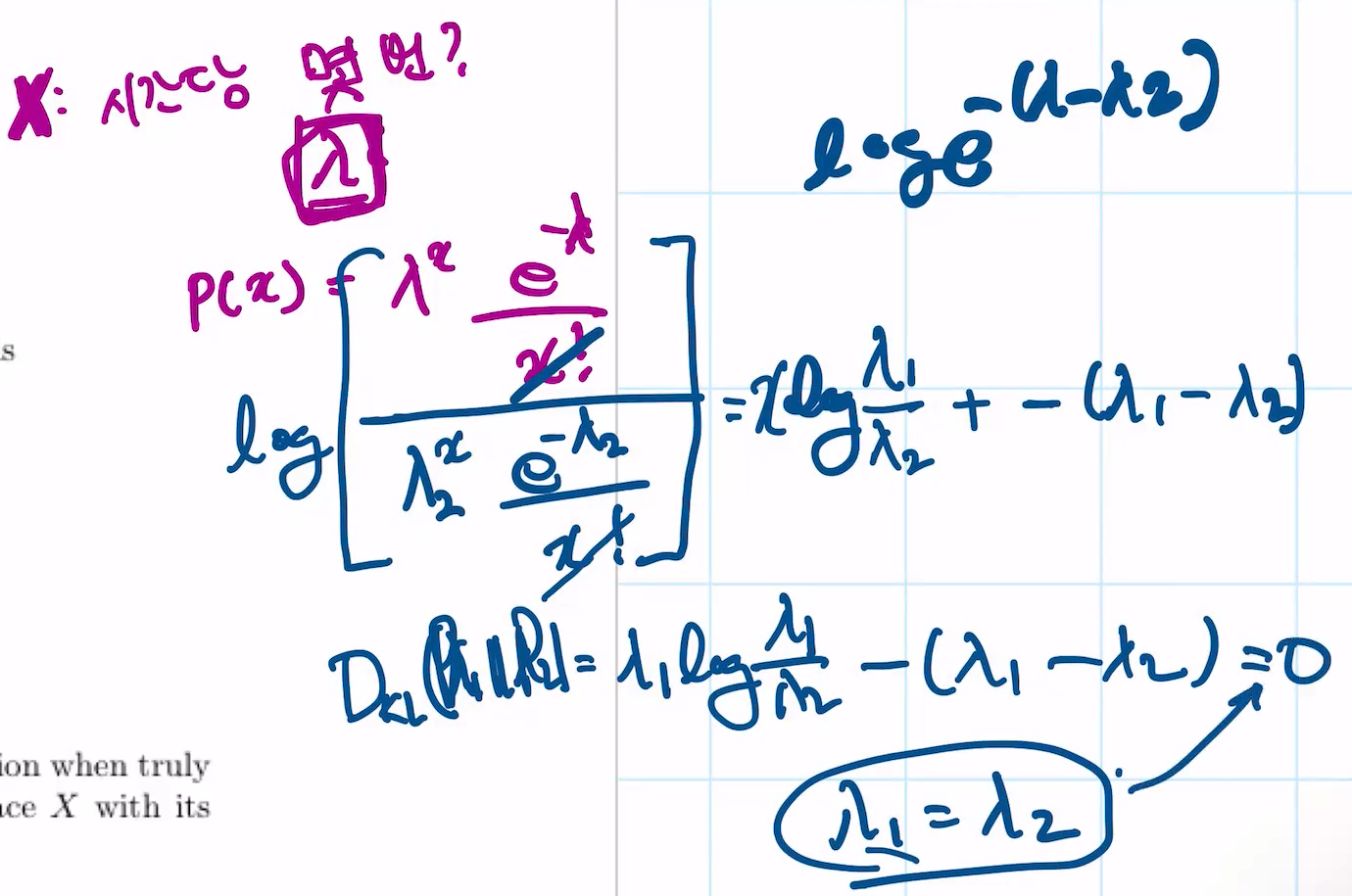
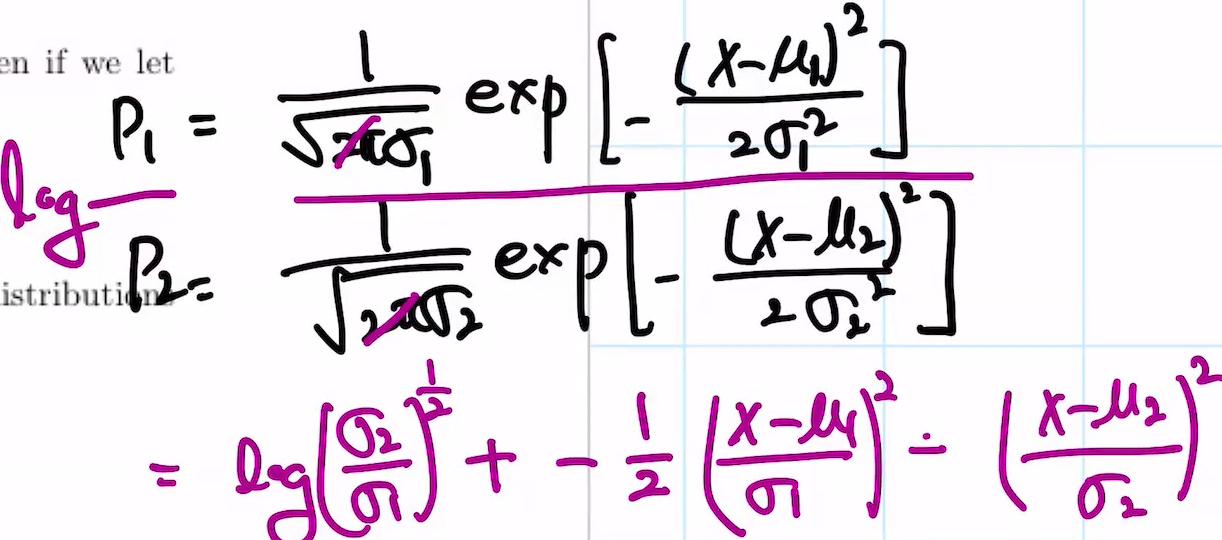
이 때, 위의 E X~p1은,

시험에 나온다 함.

왜 DKL(P||Q) > 0일까?

이는 Jensen's inequality로 풀 수 있음

이걸 잘 해석하면 아래가 됨.

 

f가 convex일 때, 각 point의 func값은 각 point의 func값의 linear combination보다 작거나 같음.

반대로 f가 -log 취하면 반대임.

 

람다i를 pi로 바꿔도 됨. 이는 일종의 기대값이 됨. x는 p에 대한 기대값.

 

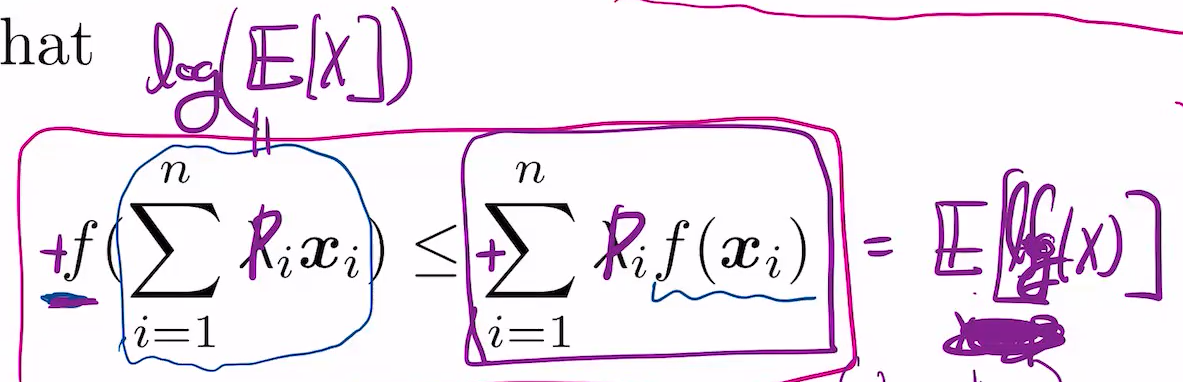
-DKL(p||q) = 

 

 

MLE(Maximum Likelihood Estimation)

이를 구하는 법

 

 

 

 

y를 집어넣으면 남는건 parameter.

density에 parameter 집어넣고 theta에 대해 maximize.

 

 

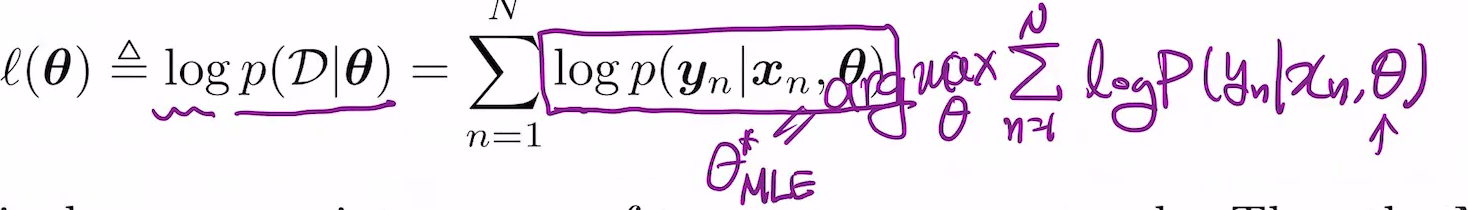
p자리에 Pd를 넣으면, 그리고 q자리엔 우리가 선택한 distribution density function을 넣으면

이 때, theta1 + ... + theta3 = 1이고, 각 theta는 0과 같거나 큼.

theta3 = 1-theta1-theta2를 P(D)에 넣고 계산.

그러면 

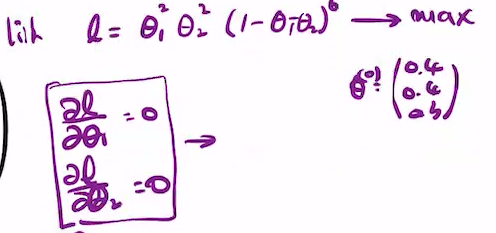
이때 Lagrangian is as follows 밑의

첫번째항은 negative loglikelihood, 두번째항은 constraint, 그리고 감마는 라그랑주 멀티플라이어. 이것들을 조합한 식 L(..)는 더미배리어블로 람다가 포함됨. 

람다만으로 표현된 로스펑션 구할 수 있음. 이게 dual p이고, min -sigma NklogThetak subfect to theta1+theta2+theta3=1, 세 세타 다 nonnegative.

Y~cat(hat theta nle) = prediction.

 

univariate gaussian

y1~yn 여러개 관측. 다음에 뭐가 나올지 모델로 만들고자 함.

likelihood는 y1에 대한 라이클리후드는 아래.

여기에

 

 

이것들도 곱해가는

 

 

이건 뮤와 시그마에 대한 펑션.

 

 

 

시그마는 로그 안에 들어있음. 그래서 역행렬로 풀 수 없나? 아님. 뮤부터 보면 됨. 그렇게 해서 풀기 전, NLL을 고려하면 아래철첨 됨.(원래는 loglike = -N...)

하고나면 나오는게 4.2.5의 이 식.

 

 

 

저 위의 -loglike = +N... 을 미분하면

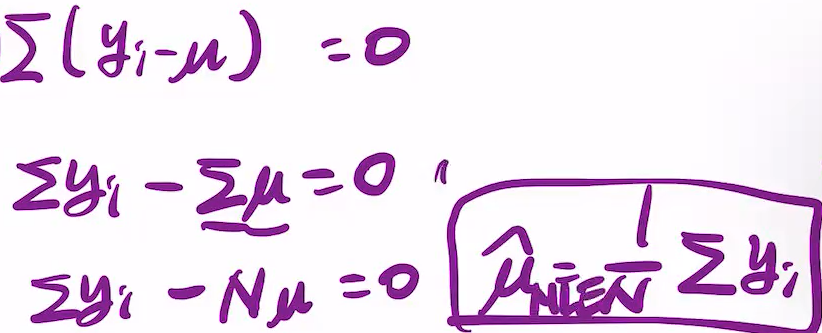
가 나오고, sigma에 대한 건 이걸 저 식에 집어넣고 풀면 됨.

미분하고 넣으면 ,sample variance가 나옴.

 

 

 

 

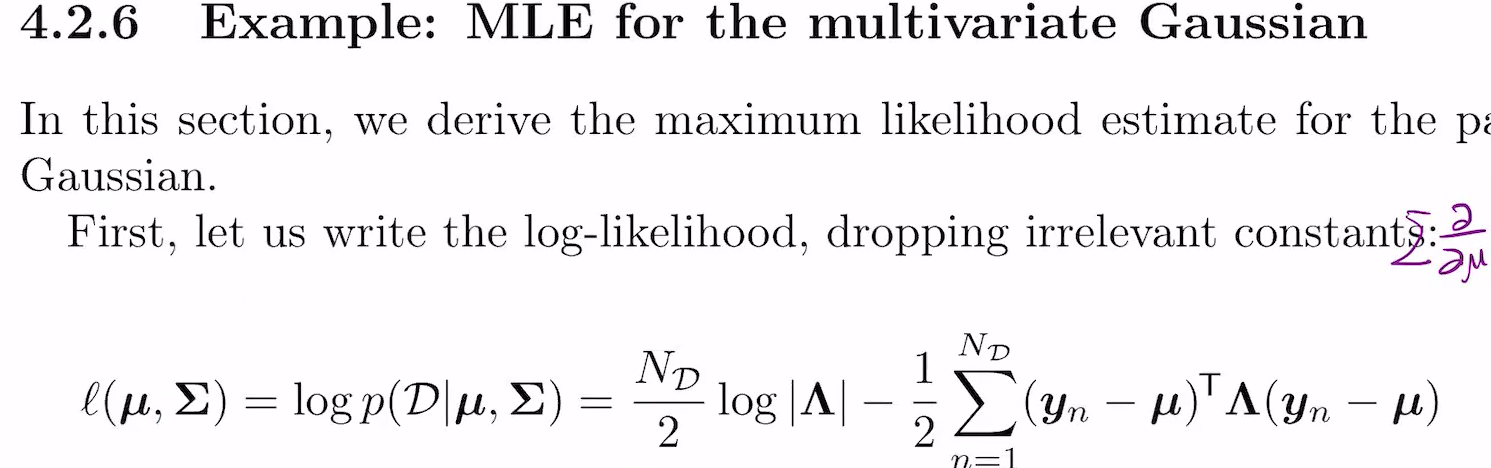
y1 y2축이 있음. 여기에서 하나가 값이 있다 하자.

그럼 covariance행렬보다 precision행렬(A같이 생긴거) 쓰는게 나음. 왜? inverse 안 붙여도 되서.

결론은 mean의 maximum likelihood estimation은 sample mean이 되고,

cov의 mle는 sample covariance가 됨. 그 유도과정은 벡터메트릭스 행렬에 대한 미분법을 알면 유도 가능.