히스토그램(한 영상의 어두운 정도) 계산법 : 그냥 일일이 화소 하나씩 다가가며 그 밝기 보고, 이를 계산해가면 됨
그 다음에 정규화때리기
이 히스토그램을, 영상 품질 개선에 쓴다(히스토그램 평활화).
명암 l을 기준으로, 그보다 작은 명암을 갖는 화소의 비율을 l/L 로 만드는 함수.

위의 식을 응용해, 히스토그램의 누적분포함수를 이용해 픽셀의 분포를 재배치하는 것이 히스토그램 평활화이다.

M과 N은 영상의 가로, 세로(즉, 픽셀 수)
cdf(v)는 해당 밝기값에서의 cdf값. 즉, 해당 밝기에서의 누적분포함수 값.
이를 이용해, cdf의 기울기가 1보다 큰, 발생빈도가 높은 곳은 기울기가 급격해지며,
발생빈도가 낮은 곳은 반대의 경우를 이용해, 편중된 밝기값을 분산시키고, 흩어진 밝기값을 좁게 모이게 한다.
cdf중 최솟값을 cdfmin에 넣고, L은 최대밝기값 255를 대입한다.
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
/*
1. 히스토그램 계산
2. 히스토그램 빈도값에서, 누적빈도수를 계산
3. 누적빈도수를 정규화
4. 결과화소값 = 정규화 누적합 * 최대화소값에 맞춘다
*/
void calc_Histo(const Mat& image, Mat& hist, int bins, int range_max = 256)
{
int histSize[] = { bins }; // 히스토그램 계급개수
float range[] = { 0, (float)range_max }; // 히스토그램 범위
int channels[] = { 0 }; // 채널 목록
const float* ranges[] = { range };
//image - 계산할 이미지 배열
//nimages - 배열에 보함된 이미지 수
//히스토그램 계산할 채널 번호 배열(BGR의 경우, B는 0, R은 2, 지금은 그레이이므로 0)
//히스토그램 계산할 영역 지정. Mat()은 영역지정 x
//hist - 히스토그램 계산결과
//histsize - 빈도수 분류할 칸의 개수
calcHist(&image, 1, channels, Mat(), hist, 1, histSize, ranges);
}
//히스토그램 그리는 함수
void draw_histo(Mat hist, Mat& hist_img, Size size = Size(256, 200))
{
hist_img = Mat(size, CV_8U, Scalar(255));
float bin = (float)hist_img.cols / hist.rows;
normalize(hist, hist, 0, size.height, NORM_MINMAX);
for (int i = 0; i < hist.rows; i++)
{
float idx1 = i * bin;
float idx2 = (i + 1) * bin;
Point2f pt1 = Point2f(idx1, 0);
Point2f pt2 = Point2f(idx2, hist.at <float>(i));
if (pt2.y > 0)
rectangle(hist_img, pt1, pt2, Scalar(0), -1);
}
flip(hist_img, hist_img, 0);
}
void create_hist(Mat img, Mat& hist, Mat& hist_img)
{
int histzise = 256, range = 256;
calc_Histo(img, hist, histzise, range);
draw_histo(hist, hist_img);
}
int main()
{
Mat image = imread("img/test_nanami.jpg", 0); //영상 읽기
CV_Assert(image.data);
Mat hist, dst1, dst2, hist_img, hist_img1, hist_img2;
create_hist(image, hist, hist_img); //히스토그램 및 그래프 그리기
//히스토그램 누적합 계산
Mat accum_hist = Mat(hist.size(), hist.type(), Scalar(0));
accum_hist.at<float>(0) = hist.at<float>(0);
for (int i = 1; i < hist.rows; i++) {
accum_hist.at<float>(i) = accum_hist.at<float>(i - 1) + hist.at<float>(i);
}
accum_hist /= sum(hist)[0];
accum_hist *= 255;
dst1 = Mat(image.size(), CV_8U);
for (int i = 0; i < image.rows; i++) {
for (int j = 0; j < image.cols; j++) {
int idx = image.at<uchar>(i, j);
dst1.at<uchar>(i, j) = (uchar)accum_hist.at<float>(idx);
}
}
equalizeHist(image, dst2);
create_hist(dst1, hist, hist_img1);
create_hist(dst2, hist, hist_img2);
imshow("User_hist", hist_img1), imshow("dst1_User", dst1);
waitKey();
return 0;
}
이진 영상
한 영상을 임계값(T)보다 크면 흑, 아니면 백으로 바꾸는 방식.
픽셀을 두 부류로 나누고, 두 부류의 명암 분포를 반복해서 구하여
가장 두 부류의 명암 분포를 균일하게 하는 경계값을 선택한다. 해당 Threshold를 구하는 것.
따라서, 모든 픽셀을 기준으로 Threshold를 구해야 하기에, 속도가 느리다.
전체 해 공간이 0~L-1의 L개의 점을 가진 1차원 공간이다. 또한, 두 개의 가중치와 두 개의 분산을 L번 계산해야 하는데, 따라서 시간복잡도는 O(L^2)이다.
분산이 작을 수록 균일성이 크므로, 이것이 작은 것이 중요하다. 즉, 한 T를 기준으로, 왼쪽의 분산과 오른쪽의 분산의 차이가 작게 하는 것이 중요할 것이다.
threshold(본래 이미지, 리턴할 이미지, 100, 255, THRESH_OTSU);로 손쉽게 구현이 가능하다. 혹은 이진화 기법 역시 가능한데, THRESH_BINARY로 바꾸면 된다.
간단 알고리즘은
1. 정규 히스토그램을 만든다
2. 명암이 0일 때의 히스토그램 / M*N과 그 명암일 때의 평균값(즉, i=0이 곱해지므로 무조건 0이 됨)을 구한다
for(t = 1 to L-1) {
w0(t) = w0(t-1) + 명암이 t일 때의 히스토그램 / M*N
m0(t) = w0(t-1)m0(t-1) + (t*명암이 t일 때의 히스토그램 / M*N, 즉 평균)
m1(t) = (m - w0(t)m0(t))/(1-w0(t)
을 구한다.
다음으로, Vbetween(t) = w0(t)(1-w0(t))(m0(t)-m1(t))^2의 분산을 계산한다.
}
앞의 for문에서 가장 큰 Vbetween이 임계값이 되며, 이를 바탕으로 이진화한다.
연결 요소
4연결성 - 4방향 기준으로 붙어있는 애들은 같은 번호를 갖는다
8연결성 - 8방향 기준으로 붙어있는 애들은 같은 번호를 갖는다
이 붙어있는 애들을 찾아 번호를 붙이는 것이 범람채움 알고리즘.
알고리즘 자체는 그냥 단순히 dx, dy를 활용한 bfs로 만들 수 있으니 pass
여러 연산

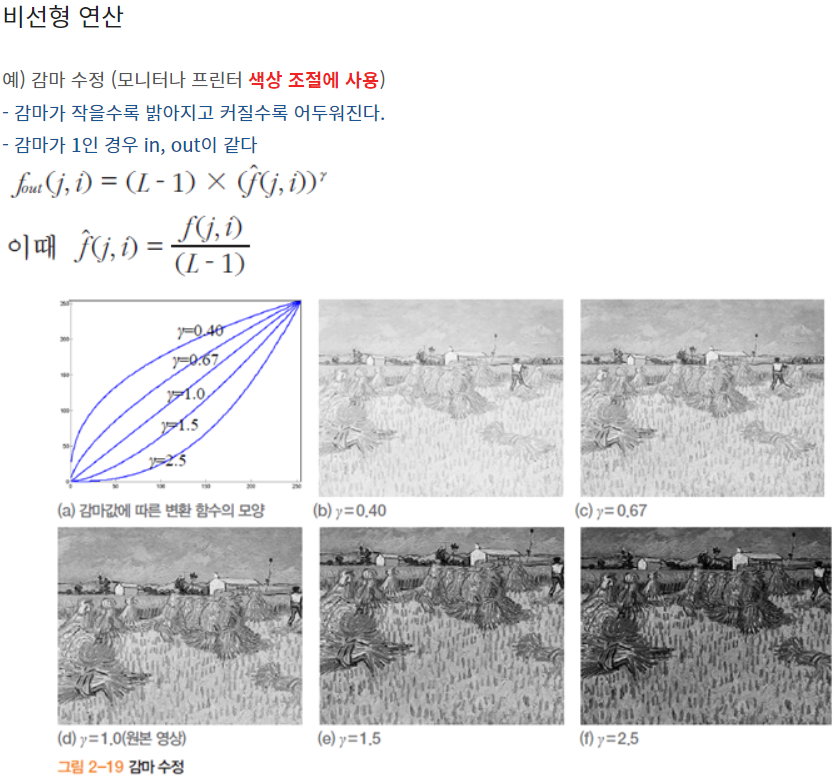

영역 연산
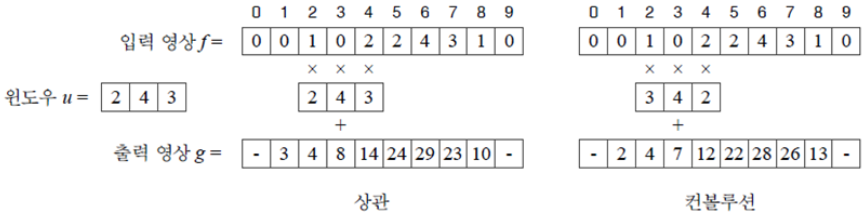

컨볼루션의 경우, 상관과 달리 윈도우를 뒤집어 실행하므로, 실제 값은 윈도우가 더욱 잘 적용되게 나옴.
또한, 1차원에서 보듯이 가장자리는 계산을 되도록 안한다.

수식은 다음과 같이 나온다.
이러한 마스크는 어떠한 것을 쓰느냐에 따라 바뀐다.
정규마스크는 박스마스크로 불리며, 주위 9개의 화소의 평균을 구하고, 합이 1이 되도록 정규화한다.
가우시안 마스크는 표준편차가 0.5이며, 화소로부터의 거리에 따라 가중치를 부여한다.
그 외 마스크의 특징이다.

기하변환
pass
양선형 보간
선형 보간: 값을 아는 두 점 P, Q 사이의 모르는 값 R을,
P, Q의 값과 거리비를 이용해 구한다.

그니까 양선형은 두 번 적용하여, 네 개의 인접한 점과 그에 따른 면접을 통해 구한다.

어떠한 영상을 n배 확대할 때, 어떤 픽셀은 원 영상의 값을 그대로 못 받게 될 것이다.
이 때 쓰는 것이다. 밑의 그림에서 파란 부분이 원 영상으로부터 값을 받는 곳,
나머지는 확대로 인해 비어버린 부분이다. 여길 양선형 보간으로 채운다.

void bilinear(Mat& image1, Mat& image2, int rate) {
for (int y = 0; y < image2.rows; y++) {
for (int x = 0; x < image2.cols; x++) {
int px = (int)(x / rate);
int py = (int)(y / rate);
double fx1 = (double)x / (double)rate - (double)px;
double fx2 = 1 - fx1;
double fy1 = (double)y / (double)rate - (double)py;
double fy2 = 1 - fy1;
double w1 = fx2 * fy2;
double w2 = fx1 * fy2;
double w3 = fx2 * fy1;
double w4 = fx1 * fy1;
//흑백영상
if (image1.channels() == 1) {
uchar P1 = image1.at<uchar>(py, px);
uchar P2 = image1.at<uchar>(py, px + 1);
uchar P3 = image1.at<uchar>(py + 1, px);
uchar P4 = image1.at<uchar>(py + 1, px + 1);
image2.at<uchar>(y, x) = w1 * P1 + w2 * P2 + w3 * P3 + w4 * P4;
}
//컬러영상
else if (image1.channels() == 3) {
Vec3b P1 = image1.at<Vec3b>(py, px);
Vec3b P2 = image1.at<Vec3b>(py, px + 1);
Vec3b P3 = image1.at<Vec3b>(py + 1, px);
Vec3b P4 = image1.at<Vec3b>(py + 1, px + 1);
image2.at<Vec3b>(y, x) = w1 * P1 + w2 * P2 + w3*P3 + w4 * P4;
}
}
}
}
int main()
{
Mat image = imread("img/test_nanami.jpg", -1); //영상 읽기
CV_Assert(image.data);
Mat retimg;
int h = image.rows;
int w = image.cols;
int imgcstate = (image.channels() == 1) ? CV_8UC1 : CV_8UC3;
Mat outimg(h, w, imgcstate, Scalar(0));
int scale = 5;
bilinear(image, outimg, scale);
imshow("original", image);
namedWindow("output", WINDOW_AUTOSIZE);
imshow("output", outimg);
waitKey(0);
return 0;
}
다해상도
이미지를 줄일 때의 식.

그러나 위는 에일리어싱이 발생하기에, 다운샘플링 이전에 스무딩을 적용하기도 한다.
다섯 화소의 가중치 곱의 합을 계산하며, 가중치 역할을 하는 w(스무딩 커널)이 핵심.

파이썬 용
위는 그냥, 아래는 가우시안 필터 활용
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
#플롯이므로, 이미지는 모두 같은 크기로 나옴
def down_sample(img) :
out_h, out_w, c = img.shape
out_h//=2
out_w//=2
down_img = np.zeros([out_h, out_w, c], dtype = np.uint8)
for y in range(out_h):
for x in range(out_w):
down_img[y, x] = img[y*2, x*2]
return down_img
img = cv.imread('Data/test_nanami2.png')
if img is None:
print('Image Load failed')
exit()
img = cv.cvtColor(img,cv.COLOR_BGR2RGB)
#shape : 높이, 너비, 채널의 3개짜리 list
#이중 더 작은 값을 min_axis로 대입
min_axis = np.minimum(img.shape[0],img.shape[1])
#16size 이하일 경우엔 1회, 아니라면 log취해서 2배일 때마다 1씩 추가
if np.log2(min_axis) > 4 :
iteration = int(np.log2(min_axis)-4)
else:
iteration = 1
pyramid = []
pyramid.append(img)
subplot_y = (iteration+1)//3 # subplot 지정, 원본도 plot 하기위해 +1, 한 행당 3개의 그림 plot.
if (iteration+1) %3 >0: # 3으로 나눠떨어지지 않으면 행 추가
subplot_y+=1
#submun = 231
#subplot : 한 화면에 여러개의 그래프를 보이게 함
sub_num = subplot_y*100 + 31
fig = plt.figure(figsize=(10,6))
plt.subplot(sub_num)
plt.imshow(pyramid[0])
for i in range(iteration):
pyramid.append(down_sample(pyramid[i]))
plt.subplot(sub_num+i+1)
plt.imshow(pyramid[i+1])
fig.tight_layout()
plt.show()
#스무등 연산 추가
def gaussian_smooth(img):
#원 이미지, (커널 사이즈), x방향 시그마
smooth = cv.GaussianBlur(img, (5,5), 0)
out_h, out_w, c = img.shape
out_h //= 2
out_w //= 2
down_img = np.zeros([out_h, out_w, c], dtype = np.uint8)
for y in range(out_h):
for x in range(out_w):
down_img[y, x] = smooth[y * 2, x * 2]
return down_img
gaussian_smooed_pyramid = []
gaussian_smooed_pyramid.append(img)
#figure : plt의 사이즈 지정
#subplot : plt 내에 위치 지정
#imshow : 이미지를 plt에 등록
fig = plt.figure(figsize=(10, 6))
plt.subplot(sub_num)
plt.imshow(gaussian_smooed_pyramid[0])
for i in range(iteration):
gaussian_smooed_pyramid.append(gaussian_smooth
(gaussian_smooed_pyramid[i]))
plt.subplot(sub_num+i+1)
plt.imshow(gaussian_smooed_pyramid[i+1])
#가장자리 별로 없게 이미지 배치
fig.tight_layout()
plt.show()정리
1) 히스토그램: 명암값이 나타난 빈도수. 이는 영상 특성 파악이 가능하다.
1-1) 정규화 작업을 통해, 특정 영역에 몰려있는 픽셀값을 최소~최대값으로 나눠준다.
2) 히스토그램 평활화를 통해, 영상 품질 개선이 가능하다.
2-1) 특정 영역에 집중되어 있는 분포를 균등분포함수로, 골고루 분포하도록 하는 작업
2-2) 각각의 값이 전체 분포에 차지하는 비중에 따라 분포를 재분배하는, 명암 대비 개선
3) 이진화는, 오츄 알고리즘을 쓰는데, 이는 각 집합의 명암분포가 균일할수록 좋다는 점에 착안, 균일성이 큰 임계값 t를 기준으로 이진화시키는 것이다.
'버츄얼유튜버' 카테고리의 다른 글
| 비전 3) 에지 검출 (0) | 2021.12.15 |
|---|---|
| GAN) batch normalization (0) | 2021.12.14 |
| 비전 1) 봐두면 좋은 논문 및 긍/부정 부류, DB (0) | 2021.12.13 |
| GAN의 G와 D 객체 (0) | 2021.12.13 |
| 손실함수 (0) | 2021.12.13 |

