6장은, 관심점이나 영역으로부터, d차원 공간의 한 점인 특징벡터 x를 추출하는 장.
예를 들어, SIFT기술자의 x는 128차원 공간의 점.
그렇다면 이 공간에 있는 두 점 a와 b를 매칭하려면? 이들이 얼마나 떨어져있는지 측정하는 거리 척도가 필요.
두 점은 각각 a=(a1, a2... a128)과 b=(b1, b2,....b128)이 된다. 이는 유클리디안 거리로 측정하는데, 이는
d_e(a,b) = ||a-b|| = sqrt(sigma(from i=1 to d) { (ai-bi)^2 }로 표현 가능.
그러나 확률분포에서, 여러 점 중 어떤 것이 특정 점과 더 가까운지 비교하는 과정에서,
확률분포 상 발생할 확률이 크지만 특정 점과 먼 경우와, 발생할 확률이 작지만 특정 점과 가까운 경우를 비교하자.
이러면 전자가 더 가깝다고 말해야 합리적일 것이다. 이를 고려한 것이 마할라노비스거리로, 점 a에서 가우시안분포 N(mu, sigma)까지를 이른다. 이 떄 Σ는 공분산이고, μ는 평균벡터다.

전처리 단계에서 화이트닝 변환을 통해 공분산 행렬을 단위행렬로 만들어, 마할라노비스 거리 대신 유클리디안 거리를 활용하는 것도 가능.
이렇게 거리를 구하는 법을 알았으니, 매칭을 사용하는 법을 알아보자. 가령 스테레오 영상이나 파노라마 여앙에서 쓰일 것이다.
두 장의 영상을 매칭할 때, 첫 번째 영상의 특징벡터를 ai(i<=i<=m), bj(1<=j<=n)이라 하자. 가장 단순한 매칭전략은 고정 임계값을 쓰는 것이다. 서로 다른 두 영상에서 추출한 점 두 개가
d(ai, bj) < T ,이 때 d는 유클리디안 or 마할라노비스를 만족하면 성공적으로 매칭되었다고 가정한다.
T를 작게 하면 가까운 쌍만 매칭하고 거리가 먼 진짜 매칭 쌍은 실패하는 거짓부정이 발생할 수 있고,
크게 하면 거리가 먼 애들도 성공하지만, 반대로 가짜인데도 매칭되는 거짓긍정이 발생 가능.
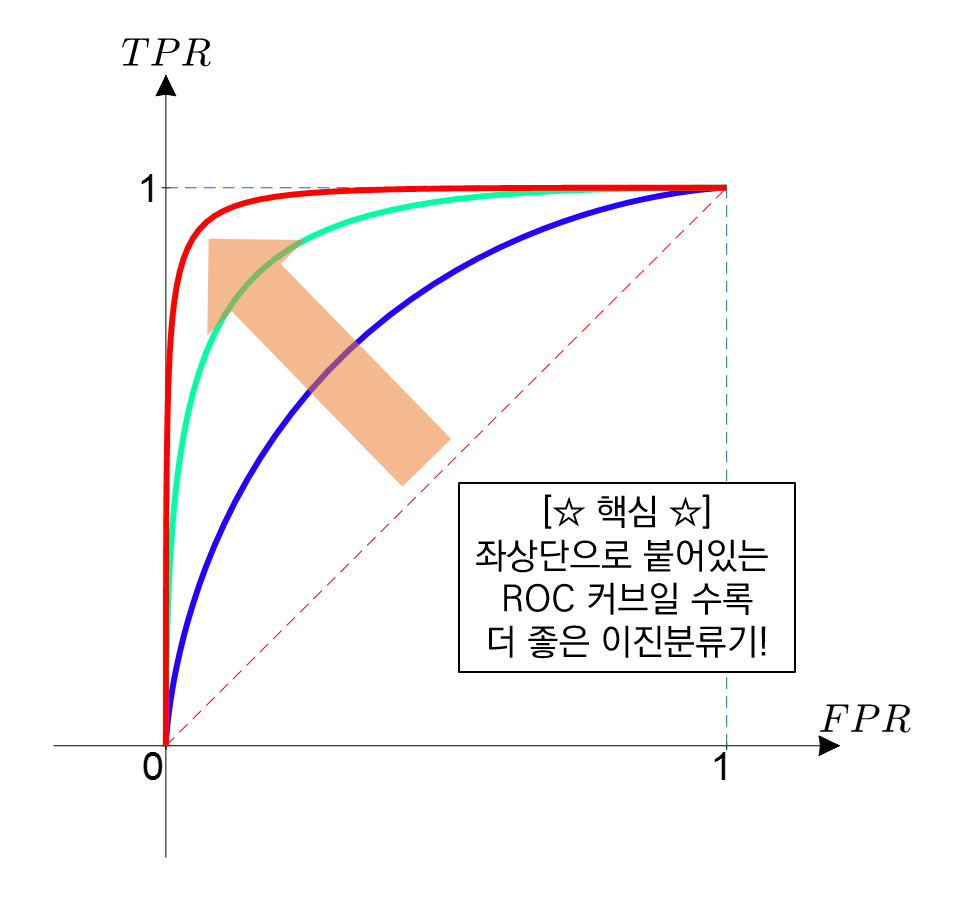
T를 점차 크게 하며 수집한 점 (FPR, TPR)을 이은 곡선이 ROC(Reciever Operating Characteristic)곡선이라 한다.
이 때 TPR = 참 긍정률 = TP/(TP+FN)
FPR = 거짓 긍정률 = FP/(FP+TN)
빠른 최근접 이웃 탐색
순진한 매칭 알고리즘 : 첫 영상 특징벡터 ai와 두번쨰 영상 특징벡터 bi를 일일이 비교하면서, threshold보다 dist가 작으면 vector에 넣는 것. 그냥 평범한 n^2짜리 알고리즘.
이를 더 빠르게 개조한 것들론, 이진검색 트리를 개조한 kd트리 & 해싱을 개조한 위치의존
빠른매칭 알고리즘
mlist = {}
for i=1 to m {
kd트리나 해싱알고리즘으로 ai의 (근사)최근접 이웃 b_match 탐색
if d(ai, b_match) < T then mlist = mlist + (ai, b_match)
}이를 kd트리로 개조해보자.
n개의 특징벡터 X={x1, x2, ..., nx}으로 kd트리를 만든다 하면, 하나의 특징벡터는 xi={x1, x2,.... xd}로 표현되는 d차원 벡터다. kd트리는 하나의 벡터가 하나의 노드가 되어, 루트노드는 X를 두 개의 부분집합 X_left와 X_right로 분할한다.
이 분할의 기준은, 우선
1) d개의 차원(축) 중, 어느 것을 쓸 것인가? 보통 분할 효과를 극대화하기 위해, 각 차원의 분산을 계산한 후, 최대 분산을 갖는 축 k를 선택.
2) 다음으로, 축을 선택했으니 n개의 샘플 중 어느 것을 기준으로 X를 분할할지 결정. X_left와 X_right를 크기를 같게 해 균형잡힌 트리를 만들기 위해, X를 차원 k로 정렬하고, 그 결과의 중앙값을 분할 기준으로 만든다.
이렇게 X_left, X_right를 만든 다음, 이 둘 각각에 대해 또 나누는 재귀를 반복하여 kd트리를 완성한다.
T = make_kdtree(X);
func make kdtree(X) {
if x is not null:
return Nil;
elif len(X) == 1 :
트리노드 node 생성
node.vector = x_m (X내의 벡터)
node.leftchild = node.rightchild = Nil
return node
else:
d개의 차원 각각에 대해 X분산을 구하고, 최대 분산 갖는 차원 k
X를 k차원 기준으로 정렬해 X_sorted 구함
X_sorted에서 중앙값을 x_m, 왼쪽과 오른쪽 부분집합 X_let, X_right라 한다
트리노드 node 생성
node.dim = k #어느 차원으로 분할하는지
node.vector = x_m #어떤 특징벡터로 분할하는지
node.leftchild = make_kdtree(X_left)
node.rightchild = make_kdtree(X_right)
reurn node
}자세한 건 책의 예제 보라
kd트리를 이렇게 만들었다. 그럼 새로운 특징벡터 x를 입력하면, 이의 최근접이웃은 어떻게 찾나? 이 역시 책 보라.
수도코드는 아래
stack s #백트래킹 위해, 지나온 노드 저장할 스택 생성
curr_best = INF
nearest = Nil
search_kdtree(T, x) # t:kd트리, x: 탐색할 특징벡터
func search_kdtree(T, x) :
t = T
while (not is_left(t)): #단말노드 찾음
if x[t.dim] < t.vector[t.dim]
s.push(t, "right")
t = t.leftchild
else:
s.push(t,"left")
t = t.rightchild
d = dist(x, t.vector)
if d < curr_best:
curr_best = d
nearest = t
while (s is not null): #거쳐온 노드 각각에 대해 최근접 가능성 여부를 확인(백트래킹)
(t1, other_side) = s.pop()
d = dist(x, t1.vector)
if d < curr_best:
curr_best = d
nearest = t1
if x에서 t1의 분할평면까지 거리 < curr_best: #건너편에 더 가까운게 있을 수 있다
t1의 otherside 자식노드를 t_other라 할 때,
search_kdtree(t_other, x)근사최근접이웃은 더 효율적으로 계산할 수 있다. 힙에 있는 모든 노드를 조사하지 않고, try_allowed라는 매개변수를 이용해 조사횟수를 제한하며, 이 안에 조사해서 찾은 것을 답으로 취한다. Muja2009이며, 매칭을 빠르게 해야하는 경우에 유용하며 최근접이웃을 찾는 것과 별 차이도 없다.
heap s #백트래킹 위해, 지나온 노드 저장할 스택 생성
curr_best = INF
nearest = Nil
try = 0 #비교횟수
search_kdtree(T, x) # t:kd트리, x: 탐색할 특징벡터
func search_kdtree(T, x) :
t = T
while (not is_left(t)): #단말노드 찾음
if x[t.dim] < t.vector[t.dim]
s.push(t, "right")
t = t.leftchild
else:
s.push(t,"left")
t = t.rightchild
d = dist(x, t.vector)
if d < curr_best:
curr_best = d
nearest = t
try++
if try > try_allowed :
break
while (s is not null): #거쳐온 노드 각각에 대해 최근접 가능성 여부를 확인(백트래킹)
(t1, other_side) = s.pop()
d = dist(x, t1.vector)
if d < curr_best:
curr_best = d
nearest = t1
if x에서 t1의 분할평면까지 거리 < curr_best: #건너편에 더 가까운게 있을 수 있다
t1의 otherside 자식노드를 t_other라 할 때,
search_kdtree(t_other, x)
해싱은 더 많은 메모리, 더 짧은 계산시간이다.
실수 여러개로 구성된 특징벡터 x=(x1, x2... xn) 에서, (근사)최근접이웃을 찾는 것이 목표.
위의 것과 다르게, 골고루 퍼뜨림 안되며, 서로 가까운 특징 벡터는 같은 통에 담길 확률이 크고, 그렇지 않으면 낮아야 한다. 가까운 벡터끼리 충돌을 일으킬 확률을 높여야 한다. 그래야 같은 통에서 최근접이웃을 찾을수 있기 때문.
위치의존해싱(Andoni 2008)이 널리 쓰인다.
H가 여러 해시 함수의 집합일 때, 이를 여러 개 선택해 결합해서 쓴다. H에서 뽑힌 해시 함수가 아래의 식을 만족하면 H를 위치의존적이라 한다. p(.)는 확률이며, ||a-b||는 a와 b 사이의 유클리디안 거리임을 유의
임의의 두 점 a,b에 대해
||a-b|| <= R이면 p(h(a) = h(b)) >= p1이고,
||a-b|| >= cR이면 p(h(a) = h(b)) <= p2이다.
이 경우, c>1, p1>p2||a-b|| <= R이란, 두 벡터가 가깝단 뜻이며, cR보다 이상이란 것은 상대적으로 멀단 것.
두 벡터가 가까우면 해시함수의 값이 같을 확률이 크다는 것.
그러나 만일 단 하나의 해시함수만 쓴다면, p1은 1에 아주 가깝고, p2는 0에 가까운 값을 설정해야 한다.
이는 비합리적이다. 여러 가능성을 조절하기 위해, 임의로 여러 해시 함수를 골라 조합해 근접 이웃을 찾을 확률을 높게 유지해야 한다. 자세히는 책 예제 보라.
위치의존 해시 테이블 구축
#입력 : 특징벡터집합 X, 해시테이블이 사용하는 해시함수 개수 k, 해시테이블개수 L
#출력 : L개 해시테이블
for j=1 to L {
for i=1 to k {
가우시안분포에 따른 난수 생성, (ri, bi) 설정
이로 해시함수 hi 생성
}
해시함수 gj = (h1, h2... hk) 만듬
}
for i=1 to n
for j = 1 to L
xi를 gj로 해싱해서 해당 주소의 통에 담음위치의존 해시 테이블에서 검색. 자세한건 Andoni2005
# 입력: L개의 해시테이블, 특징벡터 X, 매개변수 R과 N
# 출력: 근사 최근접 이웃 X_nearest
Q = null #근사최근접이웃 저장
for j=1 to L
j번째 해시테이블에서 주소 gi(x)인 통 조사
이 통에 있는 점 중 x와 거리가 R이내인 것을 Q에 추가
Q 크기가 N 넘으면 break. #이 행을 제거하면, R 이내의 모든 것을 Q에 저장
Q에서 거리가 가장 짧은 것을 X_nearset로 취함
기하 정렬과 변환 추정
이전까지의 매칭기법은 지역정보만 사용했다. 첫 영상의 특징벡터는, 두번째 영상의 특징벡터 중 자신과 가까운 것을 찾아 대응쌍을 이룬다. 이 때 이 쌍은 2차원기하변환관계를 가짐. 이 때 특징벡터가 검출된 물체가 강체라 가정할 때, 같은 물체에 속하는 다른 대응쌍의 기하변환은 앞의 것과 비슷해야 한다. 그러나 이 기하변환을 앞의 것은 고려하지 않았다.
잡음, 가림, 혼재가 있어도 잘 작동하는 기하정렬 알고리즘이 필요하다.
최소제곱법: 대응쌍의 집합 X={(a1,b1), (a2,b2),...(an,bn)} 이 있다. 이 쌍이 같은 물체에서 발생한 것이라면, 이들은 같은 기하 변환을 겪었을 것이다. 이 때, 기하변환 행렬 T = [[t11, t12, 0], [t21, t22, 0], [t31, t32, 1]]을 고려하자.
이 T는 ai를 bi'로 매핑한다.
bi' = aiT, 즉 (b'i1 b'i2 1) = (ai1 ai2 1) [[t11, t12, 0], [t21, t22, 0], [t31, t32, 1]]이 때 실제 bi와 bi'간의 오류가 발생한다. 이 오류는 sigma(from i = 1 to n) { ||bi-bi'|| ^ 2 } 로 표현될 것이다. 이 오류를 최소화하는 T를 찾는 것이 주 목적이 된다.
이는, 오류 E를 여섯 개의 매개변수 TIJ로 미분해서 얻은 도함수를 0으로 놓아 총 6개의 식을 얻는 것으로 알 수 있다. 자세한건 책참조
아무튼 최소제곱법은 아웃라이어에 취약하다. 갑자기 동떨어진 것이 엄청나게 멀리 있다면, 이것과 가까운 선분이 본래의 답으로 있어야 할 것보다 차이의 제곱이 더 작을테니까. 이 아웃라이어를 개선한 것이 M추정방법과 최소제곱중앙값.
자세한건 Stewart99, Meer91, Rousseeuw87
RANSAC - 입력이 대응점 쌍이고 출력이 기하변환인 경우
입력 X= {(ai,bi), i=1, 2, ..n} // 매칭 쌍 집합
반복 횟수 k, 인라이어 판단 t, 인라이어 집합의 크기 d, 적합 오치 e
출력 : 기하 변환 행렬 T
Q = null
for j=1 to k :
X에 세개 대응점 쌍을 임의로 선택
이들 세 쌍을 입력으로 Tj(행렬)를 추정
이들 세 쌍으로 집합 inlier을 초기화
for(이 세쌍을 제외한 X의 요소 p 각각에 대해)
if (p가 허용오차 t 이내로 Tj에 적합하면) p를 inlier에 넣는다
if |inlier| >= d: //집합 inlier가 d개 이상의 샘플을 가지면
inlier의 모든 샘플을 지우고 새로운 Tj를 계산
if Tj의 적합오류 < e:
Tj를 집합 Q에 넣음
Q에 있는 변환행렬 중 가장 좋은 것을 T로 취함매칭점수를 산정하, 이를 확률로 바꾸는 방법은 chum2005
choi2009는, RANSAC의 여러 변형과 성능평가 제시
이를 적용해 응용문제를 푼 사례는 wagner2010, Gordon2006(증강현실), 2차원에서 3차원 장면 구상 및 렌더링한 Snavely2006, 파노라마 영상제작 Brown2003
웹과 모바일 응용
Stone2010 : 얼굴인식프로그램의 낮은 성능 보이는 사례 제시 후, 정확도 개선. 영상찍은사람 GPS위치 친구관계를 인식과정에서 추가로 활용
컴퓨터모바일 미전을 모바일 환경에 적응하는 것은 IEEEE Workshop on Mobile Vison
영상 이어붙이는 알고리즘은 Szeliski2006, Zitova2003
인식과 같은 문제를 푸는 접근방법 개발ㅇ느 Avidan2010
파노라마를 제작한다. 방향을 점차 변화시켜가며 fi, i=1,2,...k라 하는 영상을 찍었다. 이들의 이음선을 찾아 자국이 남지 않도록 한다.
k개 모든 영상에서 지역특징 추출 (BY SIFT)
for i=1 to k-1:
kd트리 또는 위치의존 해싱을 이용해 f_i와 f_i+1 사이의 대응점 찾는다
RANSAC을 이용해, f_i와 f_i+1 사이의 변황행렬 Ti를 추정
번들조정을 수행해 Ti, i=1,2.....k-1를 보다 정확한 값으로 조정
Ti 정보를 이용, k개 영상을 이어붙임카메라변환은 Moons2010, Hartley2000참조.
RANSAC을 통해, 아웃라이어에 해당하는 대응점을 제거한다.
번들조정은, K-1개의 변환행렬을 동시에 살핌으로써 최적의 변환행렬을 추정한다.
Brown2003에 의하면, 번들조정이 된 영상은 위치, 회전, 크기 등ㅇ서 변화가 발생하므로, 이음선을 눈치채지 못하므로, 영상의 중앙은 1, 가장자리는 0이라는 값을 주고, 중앙에서 가장자리로 가면서 선형적으로 줄어드는 가중치함수 w.()을 이용해 두 영상을 선형결합한다. 이 괒엉에서 다중밴드결합알고리즘(Burt83b)를 활용해 에지 부근의 블러링현산을 해결한다.
하나의 피사체를 여러 구도에서 찍었을 때, 이 물체의 3차원모양을 복원하는 것은 "사진관광"이라 불림. Snavely2006, 2010에 나옴.
모든 영상에서 지역특징 추출 (BY SIFT)
kd트리 또는 위치의존 해싱을 통해 대응점을 찾음
for i=1 to k:
for j=1 to k:
if i!=j && fi와 fj사이에 대응점이 t개 이상이면:
RANSAC을 이용해, 변황행렬 Ti를 추정
T의 신뢰도가 c 이상이면 fi와 fj사이에 에지 부여
for 그래프의 연결요소 각각에 대해:
번들조정을 수행해 카메라시점과 3차원 점을 구함정리
1) 두 특징점의 매칭에는, 유사도와 거리측정 척도가 필요. 여기엔 유클리디안 거리와 마할라노비스 거리가 쓰임.
2) 또한 매칭을 하려면, 첫 번째 영상의 특징벡터 각각에 대해, 두 번째 영상에서 최근접 이웃을 구해야 함. kd-트리가 쓰일 수 있겠다.
2-1) n개의 특징벡터 X={x1, x2, ..., nx}으로 kd트리를 만든다 하면, 하나의 특징벡터는 xi={x1, x2,.... xd}로 표현되는 d차원 벡터다. kd트리는 하나의 벡터가 하나의 노드가 되어, 루트노드는 X를 두 개의 부분집합 X_left와 X_right로 분할한다.
2-2) d개의 차원(축) 중, 어느 것을 쓸 것인가? 보통 분할 효과를 극대화하기 위해, 각 차원의 분산을 계산한 후, 최대 분산을 갖는 축 k를 선택.
2-3) 다음으로, 축을 선택했으니 n개의 샘플 중 어느 것을 기준으로 X를 분할할지 결정. X_left와 X_right를 크기를 같게 해 균형잡힌 트리를 만들기 위해, X를 차원 k로 정렬하고, 그 결과의 중앙값을 분할 기준으로 만든다.
2-4) 이렇게 X_left, X_right를 만든 다음, 이 둘 각각에 대해 또 나누는 재귀를 반복하여 kd트리를 완성한다.
2-5) kd트리의 한 특징벡터 x의 최근접이웃은, 그 기준에 따라 단말노드까지 내려가면, 그 자리에 x의 최근접일 가능성이 큰 특징벡터를 만나게 된다.
3) 기하정렬과 변환추정: 앞의 방식은 지역정보만 썼지만, 잡음, 가림, 혼재에 강건하지 않다. 이에 강인한 방식은 최소제곱법, RANSAC이 있다.
3-1-1) 최소제곱법: 대응쌍의 집합 X={(a1,b1), (a2,b2),...(an,bn)} 쌍이 같은 물체에서 발생한 것이라면, 이들은 같은 기하 변환을 겪었을 것이다.
3-1-2) 기하변환 행렬 T = [[t11, t12, 0], [t21, t22, 0], [t31, t32, 1]]를 이용해, aiT = bi'로 매핑한다.
bi' = aiT, 즉 (b'i1 b'i2 1) = (ai1 ai2 1) [[t11, t12, 0], [t21, t22, 0], [t31, t32, 1]]3-1-3) 실제 bi와 bi'간의 오류 sigma(from i = 1 to n) { ||bi-bi'|| ^ 2 } 를 최소화하는 T를 찾는다.
3-1-4) 최소제곱법은, 아웃라이어에 취약하다.
3-2-1) RANSAC: 인라이어와 아웃라이어가 혼합된 샘플 집합이 주어진 상황에서, 인라이어를 찾아 모델을 적용
3-2-2) 임의의 두 개의 샘플 선택해, 직선의 방정식을 구한다.
3-2-3) 나머지 샘플에 대해, 이 모델에 적합한(이 직선 상에 있는 점) 구함
3-3-4) 이 점이 인라이어, 나머지가 아웃라이어가 된다.
'버츄얼유튜버' 카테고리의 다른 글
| 비전 9 ) 인식 (0) | 2022.01.08 |
|---|---|
| 비전 8) 기계학습 (0) | 2021.12.31 |
| 비전 6) 특징기술 (0) | 2021.12.28 |
| 비전 5) 영상 분할 (0) | 2021.12.28 |
| 비전 4) 지역특징 검출 (+ 코드) (0) | 2021.12.20 |


