
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from tqdm import tqdm
from torch.optim import Adam
from torchvision.datasets import MNIST
from torchvision.transforms import Compose, ToTensor, Normalize, Lambda
from torch.utils.data import DataLoader
# Dataset, Dataloader, Transform 정리는
# https://tutorials.pytorch.kr/beginner/data_loading_tutorial.html
def MNIST_loaders(train_batch_size = 50000, test_batch_size = 10000) :
# 샘플에 전이를 적용. 차례로 텐서화 - 정규화 - flatten 적용.
# ToTensor : 0~1 값 갖도록 정규화
# Normalize : ((mean1, mean2, ...), (std1, std2, ...)) 의 형태로, 각 값이 (X-mean)/std 로 바뀌게 됨. (https://guru.tistory.com/72)
transform =Compose([
ToTensor(),
Normalize((0.1307,), (0.3081,)),
Lambda(lambda x: torch.flatten(x))])
train_loader = DataLoader(
MNIST('./data/', train = True,
download = True,
transform = transform),
batch_size = train_batch_size, shuffle = True)
test_loader = DataLoader(
MNIST('./data/', train=False,
download=True,
transform=transform),
batch_size=test_batch_size, shuffle=False)
return test_loader, test_loader
def overlay_y_on_x(x, y) :
"""
replace the first 10 pixels of data [x] with one-hot-encoded label [y]
즉, 첫 10개 픽셀에 0을 곱하고, 하나엔 정답번째 픽셀에, 하나는 오답번째 픽셀에 색칠함으로써 정답/오답을 분류
"""
x_ = x.clone()
x_[:, :10] *= 0.0 # 모든 x에 대해, 첫 10개의 픽셀에 0을 곱함.
x_[range(x.shape[0]), y] = x.max()
return x_
class Net(torch.nn.Module):
# [784, 500, 500] 배열이 전달됨.
def __init__(self, dims) :
super().__init__()
self.layers = []
for d in range(len(dims) - 1): # 총 2번동안
# self.layers = [Layer(784, 500), Layer(500, 500)]
self.layers += [Layer(dims[d], dims[d+1]).cuda()]
def predict(self, x):
goodness_per_label = []
for label in range(10):
h = overlay_y_on_x(x, label)
goodness = []
for layer in self.layers:
h = layer(h)
goodness += [h.pow(2).mean(1)]
goodness_per_label += [sum(goodness).unsqueeze(1)]
goodness_per_label = torch.cat(goodness_per_label, 1)
return goodness_per_label.argmax(1)
# 훈련.
def train(self, x_pos, x_neg):
h_pos, h_neg = x_pos, x_neg
# 총 두 번 동안 훈련.
# Layer 클래스의 train을 진행
for i, layer in enumerate(self.layers):
print('training layer ', i, '...')
h_pos, h_neg = layer.train(h_pos, h_neg)
"""
https://pytorch.org/docs/stable/generated/torch.nn.Linear.html
self.weight : 자동적으로, (out_features, in_features)대로 가중치가 하나 만들어짐.
그 초기값은 u(-sqrt(k), sqrt(k))이며, k=1/in_features임.
그럼 nn.Linear은 y=xaT+b를 실행.
"""
class Layer(nn.Linear):
def __init__(self, in_features, out_features,
bias = True, device = None, dtype = None):
# self.in/out_features = in/out.features 등으로 접근 가능해짐
super().__init__(in_features, out_features, bias, device, dtype)
self.relu = torch.nn.ReLU()
self.opt = Adam(self.parameters(), lr = 0.03)
self.threshold = 2.0
self.num_epochs = 1000
# train시 불려오는 함수. 이 때, self.weight.T = 가중치.
# 최종 리턴 : (x의 단위행렬화) * (가중치)의 ReLU
def forward(self, x):
# 주어진 행렬의 벡터norm 반환
# keepdim에 대한 설명은 https://gaussian37.github.io/dl-pytorch-snippets/의 argmax
# keepdim 안하면 ([n1, n2, ....]) 이고 하면 ([[n1], [n2], ....]) 형태
# x.norm(2,1) = torch.norm(x, p=2, dim=1) = x의 2-norm을 1차원에서.
# 즉, X = [[768개의 요소]가 10000개] 인데, 이를 1차원([768개의 요소])의 2-norm(각 제곱의 합의 루트)을 계산해 10000개의 요소 가진 배열로 반환
xnorm = x.norm(2,1,keepdim = True)
x_direction = x / (xnorm + 1e-4) # 행렬을 그 노름(행렬의 크기)만큼 나눠 단위벡터로 만들기. 다른 벡터와 계산 시, 단위를 통일하여줌.
# print(torch.mm(x_direction, self.weight.T))
# print(self.relu(torch.mm(x_direction, self.weight.T)))
return self.relu( # x_direction(x를 일정 norm으로 나눈 것) * self.weight + bias = ([10000, 500])사이즈를 ReLU에 넣은 output을 리턴. 이를 통해, 배열에서 0이하인 값은 0으로 변경됨.
torch.mm(x_direction, self.weight.T) + # mm : MatrixMultiplication, 즉 x_direction과 self.weight.T를 곱함.
self.bias.unsqueeze(0)
)
# Net클래스에서 train을 하면 불려지는 함수.
def train(self, x_pos, x_neg):
for i in tqdm(range(self.num_epochs)): # 1000번 진행
# Forward-Forward답게, 2번 Forward를 진행
# ((X의 단위행렬화) * (가중치)의 ReLU)의 제곱의 1차원단위(가장 낮은 차원 = 1 list)의 평균
g_pos = self.forward(x_pos).pow(2).mean(1)
g_neg = self.forward(x_neg).pow(2).mean(1)
# 아래의 Loss는, pos(neg) 샘플을 각각 self.threshold보다 크게(작게) 하는 것이 목표임.
# 따라서, loss는 exp(cat([-g_pos + thre, g_neg - thre])) + 1 에 log를 취한 것의 평균
loss = torch.log(1 + torch.exp(torch.cat([
-g_pos + self.threshold,
g_neg - self.threshold]))).mean()
self.opt.zero_grad()
# 이 backward는 미분 계산을 위한 것으로,
# backpropagation이랑은 관련이 없음.
loss.backward()
self.opt.step()
return self.forward(x_pos).detach(), self.forward(x_neg).detach()
def visualize_sample(data, name = '', idx = 0):
reshaped = data[idx].cpu().reshape(28, 28)
plt.figure(figsize = (4, 4))
plt.title(name)
plt.imshow(reshaped, cmap = "gray")
plt.show()
if __name__ == "__main__":
torch.manual_seed(1234)
train_loader, test_loader = MNIST_loaders()
net = Net([784, 500, 500]) # [Layer(784, 500), Layer(500, 500)]
it = iter(train_loader) # len(it) == 1이라, 하나만 실행됨.
x, y = next(it) # x, y.size = [10000, 784], [10000]. 이 때, x는 10000개의 (28x28=784)이미지, y는 그 label
x, y = x.cuda(), y.cuda()
# x에 각각 참정보/거짓정보를 섞어 x_pos, x_neg를 생성(요주의. 다음에 다시 볼 것.)
x_pos = overlay_y_on_x(x, y)
rnd = torch.randperm(x.size(0))
x_neg = overlay_y_on_x(x, y[rnd])
# (x, 'orig'), (x_pos, 'pos), ... 로 묶어서 시각화
for data, name in zip([x, x_pos, x_neg], ['orig', 'pos', 'neg']):
visualize_sample(data, name)
# 훈련
net.train(x_pos, x_neg)
print('train error:', 1.0 - net.predict(x).eq(y).float().mean().item())
x_te, y_te = next(iter(test_loader))
x_te, y_te = x_te.cuda(), y_te.cuda()
print('test error:', 1.0 - net.predict(x_te).eq(y_te).float().mean().item())0) X = [10000, 784(28 x 28)], Y = [10000] 으로, 10000은 레이블이고 784는 이미지 사이즈. 따라서 X는 10000개의 784짜리 이미지, Y는 그 레이블. X는 나중에 reshape((28,28))을 통해 모양을 바꿔주게 됨.
0-1) 이 X[:, :10]에 * 0.0을 한다는 것은 곧 모든 X에 대해 앞의 10개 픽셀까지를 0을 곱한다는 뜻.
1) 우선 이미지 하나를 가지고 옴. 이는 0~255값을 지님.
1-2) load 과정에서 ToTensor을 통해 (0, 1) 값을 갖게 함.
1-3) 각 픽셀을 (xn - 0.1307) / 0.3081 진행. 실제로, 이렇게 한 X이미지의 본래 0인 픽셀값은 -0.4242값을 지니게 됨.
2) Net클래스의 train함수를 실행. self.layers = [Layer(784, 500), Layer(500, 500)] 이므로, 총 2번 실행됨.
3) Layer클래스의 train함수를 실행. self.num_epochs = 1000이므로, 총 1000번 실행됨.
4) g_pos/neg = self.forward(x_pos/neg).pow(2).mean(1) : ((X의 단위행렬화) * 가중치)의 ReLU)의 제곱(pow)의 1차원단위(가장 낮은 차원 = list)의 평균을 구함.
4-2) x_pos/neg가 전달되면, forward문은 ((X의 단위행렬화) * 가중치)의 ReLU)를 리턴함.
4-3) xnorm = [[768(28 x 28)개의 요소]가 10000개] 인데, 이를 1차원([768개의 요소])의 2-norm(각 제곱의 합의 루트)을 계산해 10000개의 요소 가진 배열로 반환
4-4) x_direction = 1-3 과정에서 구해진 음수~양수의 값이 분포된 x를 노름으로 나눠 '단위벡터'로 만듦. 이는 다른 이미지 등도 계산될 때 단위를 통일하기 위함일 수도.
4-5) x_direction(x를 일정 norm으로 나눈 것) * self.weight + bias = ([10000, 500]) 사이즈를 ReLU에 넣은 output을 리턴. 이를 통해, 배열에서 0이하인 값은 0으로 변경됨.

4-6) 즉, 4는 (이미지 x 가중치) 를 진행하고, 여기에 ReLU을 진행. 해당 행렬에 제곱을 하고, 평균 구하기.
5) 초기값은 x_pos == x_neg이지만 각각 threshold를 취하는 것에 따라 값이 변동됨.

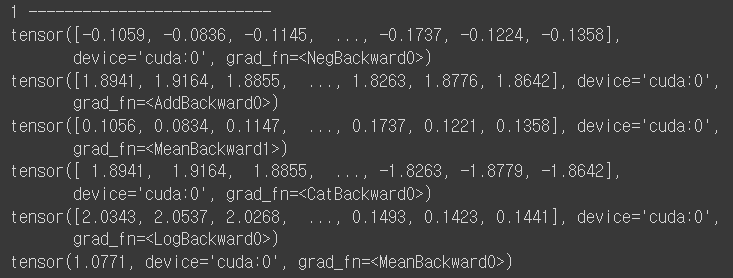
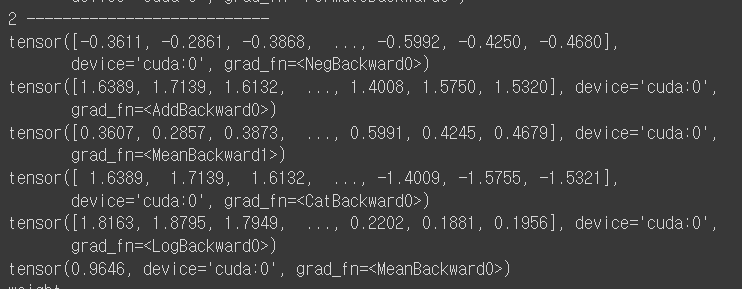
값을 보면 알 수 있겠지만, neg과 pos의 neg값의 차가 점차 커지게 된다. 그 차이는 갈수록 커짐.
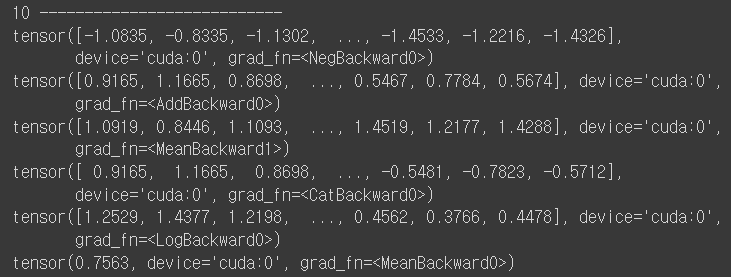
5-2) 가중치는 어째서 변경되는가? opt.zero_grad()와 loss.backward(), opt.step()을 한 번 확인해본다.
opt.zero_grad() : 역전파 단계 전에, optimizer 객체를 사용하여 (모델의 학습 가능한 가중치인) 갱신할 변수들에 대한 모든 변화도(gradient)를 0으로 만듭니다. 이렇게 하는 이유는 기본적으로 .backward()를 호출할 때마다 변화도가 버퍼(buffer)에 (덮어쓰지 않고) 누적되기 때문입니다. 더 자세한 내용은 torch.autograd.backward에 대한 문서를 참조하세요.
gradient는 말 그대로 미분임. 해당 지점의 미분값 방향으로 빼야 하는데, backward()를 호출할 때마다 변화도는 buffer에 누적됨. 따라서 이전에 사용한 gradient가 다음 iter에도 쓰이면 안 되니, 우선 0으로 만들어줌.
다음으로 loss.backward()는
torch.autograd를 사용한 자동 미분 — 파이토치 한국어 튜토리얼 (PyTorch tutorials in Korean)
torch.autograd를 사용한 자동 미분
파이토치(PyTorch) 기본 익히기|| 빠른 시작|| 텐서(Tensor)|| Dataset과 Dataloader|| 변형(Transform)|| 신경망 모델 구성하기|| Autograd|| 최적화(Optimization)|| 모델 저장하고 불러오기 신경망을 학습할 때 가장
tutorials.pytorch.kr
를 보면 알 수 있는데, dL/d(parameter) 을 계산하는 녀석이라 한다. 그럼 그 parameter의 grad를 불러올 수 있게 됨(예시 - w.grad, b.grad).
autograd 를 사용하여 역전파 단계를 계산합니다.
이는 requires_grad=True를 갖는 모든 텐서들에 대한 손실의 변화도를 계산합니다.
이후 a.grad와 b.grad, c.grad, d.grad는 각각 a, b, c, d에 대한 손실의 변화도를 갖는 텐서가 됩니다.
역전파 단계: 모델의 학습 가능한 모든 매개변수에 대해 손실의 변화도를 계산합니다.
내부적으로 각 Module의 매개변수는 requires_grad=True일 때 텐서에 저장되므로,
loss.backward() 호출은 모델의 모든 학습 가능한 매개변수의 변화도를 계산하게 됩니다.
즉, requires_grad = True 처리 된 텐서에 대해서 그 Loss에 대한 변화량 da/dLoss를 계산함.
# 손실에 따른 a, b, c, d의 변화도(gradient)를 계산하고 역전파합니다.
grad_y_pred = 2.0 * (y_pred - y)
grad_a = grad_y_pred.sum()
grad_b = (grad_y_pred * x).sum()
grad_c = (grad_y_pred * x ** 2).sum()
grad_d = (grad_y_pred * x ** 3).sum()
# 가중치를 갱신합니다.
a -= learning_rate * grad_a
b -= learning_rate * grad_b
c -= learning_rate * grad_c
d -= learning_rate * grad_d
------------------------------------------------------------------------------
loss.backward()
with torch.no_grad():
a -= learning_rate * a.grad
b -= learning_rate * b.grad
c -= learning_rate * c.grad
d -= learning_rate * d.grad
# 가중치 갱신 후에는 변화도를 직접 0으로 만듭니다.
a.grad = None
b.grad = None
c.grad = None
d.grad = None위의 두 개는 같다. 또한 None이 곧 zero_grad() 과정으로 대체됨.
따라서, self.weight가 갱신되는 것을 알 수 있다. 이 때 모델 = model = torch.nn.Sequential(...)인데,
https://pytorch.org/docs/stable/generated/torch.nn.Linear.html
에서 살펴보듯 self.weight 자체가 nn.Linear() 내부의 일종의 파라미터임. 따라서 이것과 bias가 loss에 따라 갱신됨.
5-3) 해당 loss 함수는
torch.log(1 + torch.exp(torch.cat([
-g_pos + self.threshold,
g_neg - self.threshold]))).mean()로 표현할 수 있는데, 각각 threshold에 가깝게 만드는 것이 목표다. 최종적으로 x_pos는 3.6에, x_neg는 0.5에 도달하게 됨. 이 loss함수는 x_pos는 크게, x_neg는 작게 하는 것이 목표인 loss함수임. 실제 생김새를 보면,
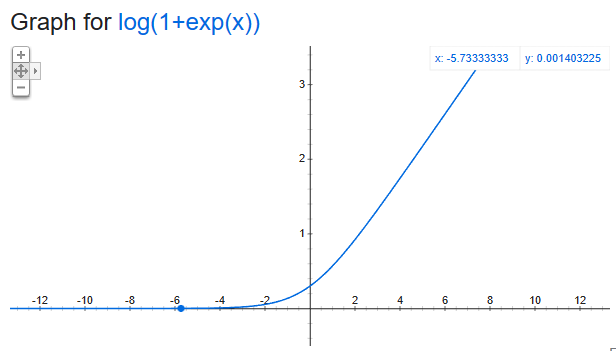
위와 같이 생긴 것을 볼 수 있다. 즉 값이 커질수록 미분값도 커지고, 작아질수록 미분값은 작아짐(절대 0은 안 됨). loss값 역시 점차 작아지게 됨. 이 과정을 통해 g_neg는 점차 작아지고, g_pos는 점차 커지게 된다.
☆ 5-4) 이렇게 하면, 각 layer의 가중치들은 neg가 들어오면 안 좋은 점수를 주고, pos가 들어오면 좋은 점수를 주는 가중치를 학습하게 됨.
6) 다음은 Net클래스의 predict함수를 함. predict는 함수를 잘 보면
def predict(self, x):
goodness_per_label = []
for label in range(10):
h = overlay_y_on_x(x, label)
goodness = []
for layer in self.layers:
h = layer(h)
goodness += [h.pow(2).mean(1)]
goodness_per_label += [sum(goodness).unsqueeze(1)]
goodness_per_label = torch.cat(goodness_per_label, 1)
return goodness_per_label.argmax(1)label 수(=10)만큼 진행하는 것을 볼 수 있다. 이는 곧 특정 이미지가 들어오면, 레이블 수만큼 돌려보면서 해당 이미지의 GT가 그 iterator label과 일치하는지 확인하는 거임.
6-1) goodness_per_label 리스트를 만든 다음, label을 붙인 h를 layer에 집어넣는다. 그렇게 하여 나오는 결과값인 goodness를 해당 리스트에 집어넣는다. 그 다음에 가장 큰 녀석을 뱉는다. 이는 곧, 특정 이미지가 해당 레이블인지 아닌지를 판단.
6-2) 'train error:', 1.0 - net.predict(x).eq(y).float().mean().item()
eq : 각 텐서의 요소(element)들을 비교해 같으면 True를, 다르면 False를 반환한다. 즉 총 10000개의 x에 대해 y와 비교해서 같은 거에 True를, 다른 거에 False를 반환하고. 이를 mean시켜서 train error을 반환함.
7) 다음으로 같은 방식으로 test를 돌려 확인.
활성화 벡터(Activation Vector) - 신경망에서 네트워크의 정점(vertex)은 뉴런이고, 단일 뉴런의 출력은 단일 값(스칼라)이다. 이 값을 활성화(activation)라고 하며, 이 네트워크 뉴런층이 출력하는 것이 곧 활성화 벡터.
로지스틱 회귀분석은 아래 글 참고
6. Learning Fast and Slow
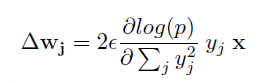
| X | 가중치 벡터 |
| yj | ReLU 결과값 |
| wj | 뉴런 j에 들어오는 가중치벡터 |
| e | learning rate |
위의 것을 말미암아 보면, 가중치 업데이트가 발생한 후 뉴런 j의 Activity의 변화량(즉, 뉴런 j에서의 출력값의 변화량)은 단순 스칼라곱 dwj.
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from tqdm import tqdm
from torch.optim import Adam
from torchvision.datasets import MNIST
from torchvision.transforms import Compose, ToTensor, Normalize, Lambda
from torch.utils.data import DataLoader
torch.set_printoptions(threshold=10_000_000)
fpos = open('recorder_pos_mm.txt', "w")
fneg = open('recorder_neg_mm.txt', "w")
# Dataset, Dataloader, Transform 정리는
# https://tutorials.pytorch.kr/beginner/data_loading_tutorial.html
def MNIST_loaders(train_batch_size = 50000, test_batch_size = 10000) :
# 샘플에 전이를 적용. 차례로 텐서화 - 정규화 - flatten 적용.
# ToTensor : 0~1 값 갖도록 정규화
# Normalize : ((mean1, mean2, ...), (std1, std2, ...)) 의 형태로, 각 값이 (X-mean)/std 로 바뀌게 됨. (https://guru.tistory.com/72)
transform =Compose([
ToTensor(),
Normalize((0.1307,), (0.3081,)),
Lambda(lambda x: torch.flatten(x))])
train_loader = DataLoader(
MNIST('./data/', train = True,
download = True,
transform = transform),
batch_size = train_batch_size, shuffle = True)
test_loader = DataLoader(
MNIST('./data/', train=False,
download=True,
transform=transform),
batch_size=test_batch_size, shuffle=False)
return test_loader, test_loader
#############################################################################
def overlay_y_on_x(x, y) :
"""
replace the first 10 pixels of data [x] with one-hot-encoded label [y]
즉, 첫 10개 픽셀에 0을 곱하고, 하나엔 정답번째 픽셀에, 하나는 오답번째 픽셀에 색칠함으로써 정답/오답을 분류
"""
x_ = x.clone()
x_[:, :10] *= 0.0 # 모든 x에 대해, 첫 10개의 픽셀에 0을 곱함.
x_[range(x.shape[0]), y] = x.max()
return x_ # x_.shape = [10000]
#############################################################################
class Net(torch.nn.Module):
# [784, 500, 500] 배열이 전달됨.
def __init__(self, dims) :
super().__init__()
self.layers = []
for d in range(len(dims) - 1): # 총 2번동안
# self.layers = [Layer(784, 500), Layer(500, 500)]
self.layers += [Layer(dims[d], dims[d+1]).cuda()]
def predict(self, x):
goodness_per_label = []
for label in range(10):
h = overlay_y_on_x(x, label) # h는, 0~9번째 까지의 픽셀에 각각 1씩 칠해진 채로 돌게 되어 goodness 결과를 낳음.
goodness = []
for layer in self.layers:
h = layer(h) #Layer클래스의 forward에 h 삽입, [10000,500] 도출. 이미 존재하는 가중치에 h를 곱해서 나온 결과가 goodness
goodness += [h.pow(2).mean(1)] # [h.pow(2).mean(1)] == [10000], 하나의 이미지의 가중치 통과 후 평균. 따라서 goodness의 사이즈 = [2 * [10000짜리 텐서]]의 리스트
goodness_per_label += [sum(goodness).unsqueeze(1)] # sum(goodness) && .unsqueeze(1) : [10000], [10000, 1]
# before : goodness_per_label = [10개의 [10000, 1]텐서] / after : [10000, 10]의 텐서. goodness_per_label을 1차원에서 합함.
goodness_per_label = torch.cat(goodness_per_label, 1)
sumcheck = []
for i in range(len(goodness_per_label)):
sumcheck.append(sum(goodness_per_label[i]))
# print(goodness_per_label)
# print(len(goodness_per_label.argmax(1)))
return goodness_per_label.argmax(1) # 최종적으로, goodness_per_label.argmax(1) 는 [7, 6, 1, ..... 0] 등 [10000]개의 이미지를 어떤 숫자인지 판가름한 것만 남게 됨.
# 훈련.
def train(self, x_pos, x_neg):
h_pos, h_neg = x_pos, x_neg
# 총 두 번 동안 훈련.
# Layer 클래스의 train을 진행
for i, layer in enumerate(self.layers):
print('training layer ', i, '...')
h_pos, h_neg = layer.train(h_pos, h_neg) # 이 부분이 있어야 i==1일 때도 train이 가능. 아니면 shape가 다르다고 뜸.
# print(h_pos, h_neg)
#############################################################################
"""
https://pytorch.org/docs/stable/generated/torch.nn.Linear.html
self.weight : 자동적으로, (out_features, in_features)대로 가중치가 하나 만들어짐.
그 초기값은 u(-sqrt(k), sqrt(k))이며, k=1/in_features임.
그럼 nn.Linear은 y=xaT+b를 실행.
"""
class Layer(nn.Linear):
def __init__(self, in_features, out_features,
bias = True, device = None, dtype = None):
# self.in/out_features = in/out.features 등으로 접근 가능해짐
super().__init__(in_features, out_features, bias, device, dtype)
self.relu = torch.nn.ReLU()
self.opt = Adam(self.parameters(), lr = 0.03)
self.threshold = 2.0
self.num_epochs = 1000
# train시 불려오는 함수. 이 때, self.weight.T = 가중치.
# 최종 리턴 : (x의 단위행렬화) * (가중치)의 ReLU
def forward(self, i, type, x):
# 주어진 행렬의 벡터norm 반환
# keepdim에 대한 설명은 https://gaussian37.github.io/dl-pytorch-snippets/의 argmax
# keepdim 안하면 ([n1, n2, ....]) 이고 하면 ([[n1], [n2], ....]) 형태
# x.norm(2,1) = torch.norm(x, p=2, dim=1) = x의 2-norm을 1차원에서.
# 즉, X = [[768개의 요소]가 10000개] 인데, 이를 1차원([768개의 요소])의 2-norm(각 제곱의 합의 루트)을 계산해 10000개의 요소 가진 배열로 반환
xnorm = x.norm(2,1,keepdim = True)
x_direction = x / (xnorm + 1e-4) # 행렬을 그 노름(행렬의 크기)만큼 나눠 단위벡터로 만들기. 다른 벡터와 계산 시, 단위를 통일하여줌.
# if type == 'pos':
# fpos.write(str(i) + ':')
# fpos.write(str(x_direction[0]) + '\n')
# elif type == 'neg' :
# fneg.write(str(i) + ':')
# fneg.write(str(x_direction[0])+ '\n')
# torchmm = torch.mm(x_direction, self.weight.T)
# if type == 'pos':
# fpos.write(str(torchmm[0]))
# elif type == 'neg':
# fneg.write(str(torchmm[0]))
# print(torchmm.shape)
return self.relu( # x_direction(x를 일정 norm으로 나눈 것) * self.weight + bias = ([10000, 500])사이즈를 ReLU에 넣은 output을 리턴. 이를 통해, 배열에서 0이하인 값은 0으로 변경됨.
torch.mm(x_direction, self.weight.T) + # mm : MatrixMultiplication, 즉 x_direction과 self.weight.T를 곱함.
self.bias.unsqueeze(0)
)
# Net클래스에서 train을 하면 불려지는 함수.
def train(self, x_pos, x_neg):
for i in tqdm(range(self.num_epochs)): # 1000번 진행
# Forward-Forward답게, 2번 Forward를 진행
# ((X의 단위행렬화) * (가중치)의 ReLU)의 제곱의 1차원단위(가장 낮은 차원 = 1 list)의 평균
g_pos_sub = self.forward(i, 'pos', x_pos).pow(2)
g_neg_sub = self.forward(i, 'neg', x_neg).pow(2)
g_pos = g_pos_sub.mean(1)
g_neg = g_neg_sub.mean(1)
# 아래의 Loss는, pos(neg) 샘플을 각각 self.threshold보다 크게(작게) 하는 것이 목표임.
# 따라서, loss는 exp(cat([-g_pos + thre, g_neg - thre])) + 1 에 log를 취한 것의 평균
loss = torch.log(1 + torch.exp(torch.cat([
-g_pos + self.threshold,
g_neg - self.threshold]))).mean()
self.opt.zero_grad()
# 이 backward는 미분 계산을 위한 것으로,
# backpropagation이랑은 관련이 없음.
loss.backward()
self.opt.step()
# detach : 기존 Tensor에서 gradient 전파가 안 되는 텐서 생성. 이는 다음레이어로 넘어갈 때 차원을 바꾸기 위함으로 학습과는 관련 x
output_pos = self.forward(i, 'else', x_pos).detach()
output_neg = self.forward(i, 'else', x_neg).detach()
# print('return -----------------')
# print(output_pos.pow(2).mean(1))
# print(output_neg.pow(2).mean(1))
return output_pos, output_neg
#############################################################################
def visualize_sample(data, name = '', idx = 1):
reshaped = data[idx].cpu().reshape(28, 28)
plt.figure(figsize = (4, 4))
plt.title(name)
plt.imshow(reshaped, cmap = "gray")
plt.show()
#############################################################################
torch.manual_seed(1234)
train_loader, test_loader = MNIST_loaders()
net = Net([784, 500, 500]) # [Layer(784, 500), Layer(500, 500)]
it = iter(train_loader) # len(it) == 1이라, 하나만 실행됨.
x, y = next(it) # x, y.size = [10000, 784], [10000]. 이 때, x는 10000개의 (28x28=784)이미지, y는 그 label
x, y = x.cuda(), y.cuda()
# x에 각각 참정보/거짓정보를 섞어 x_pos, x_neg를 생성(요주의. 다음에 다시 볼 것.)
x_pos = overlay_y_on_x(x, y)
rnd = torch.randperm(x.size(0))
x_neg = overlay_y_on_x(x, y[rnd])
# (x, 'orig'), (x_pos, 'pos), ... 로 묶어서 시각화
# for data, name in zip([x, x_pos, x_neg], ['orig', 'pos', 'neg']):
# visualize_sample(data, name)
# 훈련
net.train(x_pos, x_neg)
y_neg = y + 1
predict = net.predict(x)
eq_val = predict.eq(y)
#print(predict)
#print(y)
#print(eq_val)
print('train error:', 1.0 - eq_val.float().mean().item())
x_te, y_te = next(iter(test_loader))
x_te, y_te = x_te.cuda(), y_te.cuda()
visualize_sample(x_te, 'test')
print('test error:', 1.0 - net.predict(x_te).eq(y_te).float().mean().item())
fpos.close()
fneg.close()'블루아카이브' 카테고리의 다른 글
| PCA (0) | 2023.12.12 |
|---|---|
| HeadHunter 구조 살펴보기 (0) | 2023.01.05 |
| BERT & RoBERTa & CORD & NER (0) | 2022.12.17 |
| 에러 기록 (0) | 2022.11.18 |
| Visual Transformer (0) | 2022.08.22 |



