https://gazelle-and-cs.tistory.com/64
P vs NP 쉽게 이해하기
컴퓨터 과학에는 유명한 난제가 있습니다. 바로 P vs NP입니다. 컴퓨터 과학을 공부하다 보면 언젠간 한 번은 반드시 접하게 되는 흥미롭고도 신기한 문제인데요. 이번 포스트에서는 이에 대해서
gazelle-and-cs.tistory.com
결정문제 - 입력이 T인지, F인지만 따짐
예) 어떤 그래프와 가중치, k가 주어졌을 때, 크기가 k보다 작은 스패닝트리가 존재??
NP: 여기서 기인함.
결정론적 알고리즘(이하 결) : 분신술이 없는 모험가가 보물을 찾는다. 일일이 depth를 올리며 찾아다녀야 하기에, 무언가를 선택해야 할 때, 그 중 하나를 선택해야 다음으로 갈 수 있음. 즉, 무조건 하나의 선택만 할 수 있으며, 수행시간은 알고리즘이 끝날 때까지 수행한 단계 수
비결정론적 알고리즘(이하 비결) : 분신술이 있는 모험가. 여러 평행세계가 있으며, 병렬적으로 진행해, 어떤 입력이 참임을 알게 되면 곧 입력이 참(한 분신이 T임을 알아냄). 모든 입력이 거짓이라 판단시 입력은 거짓(F).
즉, 알고리즘 수행시간은 어떤 평행세계에서 결과를 알아낸 시간의 최댓값으로, 이 식을 우리가 세울 수는 없을 것이다.
if) 분신은 없어도 힌트가 있어서, 빠른 시간 안에 보물을 찾는다?
어떤 힌트를 따라가니 T가 나왔다면, 그 결정문제의 입력은 T일것.
반대로 어떤 힌트를 따라가니 F가 나왔다면, 그 결정문제의 입력은 F일 것.
즉, 비결을 어떤 힌트를 검증하는 결로 대체가 가능.
1) 입력이 T? 그 결이 T라 판단할 수 있는 힌트가 무조건 존재
2) 입력이 F? 그런 힌트는 없다(certificate)는 없다. 모든 평행세계는 다 F니까.
이 특징을 만족하는 결정론적 알고리즘이, 힌트를 검증하는 의미에서 verifier가 되고,
주어진 힌트는 certificate가 된다.
이 certificate는 일종의 비결이 최종적으로 생성하는 여러 평행세계중, 특정 하나로 가는 법을 알려주는 것.


비결정론적 알고리즘의 예시 - 몬테카를로
랜덤으로 점을 찍어 원의 넓이를 알아내므로, 랜덤프로세스가 포함되어 있어 출력도 그때그때 다름.
P - 결정론적 알고리즘으로 다항시간에 풀 수 있음.
NP - 비결정론적 알고리즘으로 다항시간에 풀 수 있음.
- 입력 I에 대해, 모든 certificate의 크기는 |I|의 어떤 다항식을 넘지 않는다.
- 입력 I와 어떤 certificate인 ℎ에 대해, |I|와 |ℎ|의 다항 시간에 주어진 ℎ를 검증하는 verifier가 존재한다.
certificate는 일종의 어떤 평행세계로 향하는 이정표이며, 이 수행시간은 곧 '최종적으로 생성한 모든 평행세계의 수행 시간 중 최대값'이다. 그런데 NP에 속하려면, 비결이 아항시간에 동작해야 함. 따라서, 거리가 긴 certificate는 NP의 정의에 맞지 않음.
또한 어떤 문제가 NP에 속하려면, 다항시간에 동작하는 알고리즘이 존재해야 한다. 그런데 verifier가 다항시간을 초과한다면, 이는 이미 NP에 속하지 않음.
이를 기반으로 P vs NP를 보자.
모든 결정론적 알고리즘은 비결정론적 알고리즘이다. 왜냐? 비결정론적 알고리즘은 결정론적 알고리즘이 할 수 있는 모든 걸 할 수 있으니까.
따라서

인 것이고,

인지 아닌진 모르는 것.


문제가 NP(비결정론적 다항식 시간)에 있음을 증명하려면 다음 두 가지를 표시해야 합니다:
1. **해결책에 대한 '증명' 또는 '증인'의 존재**: 이는 문제에 대한 해결책이 존재하는 경우 해당 해결책에 대한 일종의 증거나 증거를 제시할 수 있는 방법이 있어야 한다는 것을 의미합니다. 예를 들어, 스도쿠 퍼즐의 경우, 채워진 퍼즐이 인증서입니다. 채우기 퍼즐이 주어지면 솔루션이 올바른지 쉽게 확인할 수 있습니다.
2. **다항 시간 검증**: 솔루션에 대한 인증서가 주어지면 해당 인증서가 다항 시간 내에 문제에 대한 유효한 솔루션인지 여부를 검증할 수 있는 결정론적 알고리즘이 있어야 합니다. 스도쿠 예제를 계속하면 퍼즐의 크기가 다항식인 시간에 채우기 퍼즐이 유효한 솔루션(즉, 모든 행, 열 및 정사각형에 1부터 9까지의 모든 숫자가 정확히 한 번씩 포함됨)인지 확인할 수 있습니다.
문제에 대해 이 두 가지 속성을 표시할 수 있는 경우 문제가 NP에 있다는 것을 보여줍니다.
NP에 있다고 해서 문제가 빨리 해결될 수 있는 것은 아닙니다. 솔루션이 존재하면 빠르게 확인할 수 있다는 의미일 뿐입니다. NP의 모든 문제가 빠르게 해결될 수 있는지에 대한 질문은 컴퓨터 과학에서 가장 중요한 열린 질문 중 하나인 유명한 P vs NP 문제입니다.
또한 스도쿠는 백트래킹을 통해 풀며, 이는 일일이 이게 맞는건지 아닌건지 체크해야 함을 뜻.
이 때, NP-Hard와 NP-Completeness란?
어떤 특정 문제는 그 자체로 NP에 속하지만, 또한 달느 모든 NP에 비해 어렵다.
그리고 그것 중 하나만 P에 속한단 것을 알아내면 P=NP임을 알게 된다(즉, P에 속하지 않으면 P P⊊NP임).
서로 다른 문제 X와 Y가 있는데, Y의 해결법은 알고 있으나 X는 모른다 하자. 이 때,
- X의 임의의 입력을 잘 수정하면 적절한 Y의 입력을 만들 수 있고,
- 반대로 만들어진 Y의 입력을 이미 아는 방법을 이용하여 해결한 결과를 잘 조정하면 원래 X의 입력의 적절한 결과를 복원할 수 있다
고 하자. 이를 통해 X를 해결하는 경우, 이를 환산(reduction)이라고 한다고 함.
예는 최대이분매칭문제를 최대흐름문제로 환원하여 해결하는 것.
우리의 목표는 NP-Hard, 즉 NP문제 중 가장 어려운 것을 찾는 것임.
따라서, 그 문제는 모든 NP문제를 그 문제로 환산하여 해결할 수 있어야 함. 다시 말하면, 모든 NP 문제를 다항식 시간 내에 해당문제로 줄일 수 있다면 그건 NP-Hard.
문제를 완료해야 하는 작업으로, 문제의 난이도는 작업을 완료하는 데 걸리는 시간으로 생각하세요.
이제 합리적인 시간 내에 완료할 수 있는 일련의 작업(NP의 문제)이 있다고 가정해 보세요. 이러한 작업은 설거지, 방 청소, 빨래 등 일상적인 집안일과 같습니다. 어떻게 해야 하는지 알고 있고 비교적 빠르게 완료할 수 있습니다.
이제 집을 짓는 것과 같은 새로운 과제(NP-고난도 문제)가 있다고 가정해 봅시다. 이것은 일상적인 집안일보다 훨씬 더 큰 과제입니다.
모든 일상적인 집안일을 집 짓기 과제의 일부로 변형할 수 있다는 것을 보여줄 수 있다면, 집 짓기가 적어도 일상적인 집안일 중 가장 어려운 것만큼 어렵다는 것을 보여 준 것입니다. 이러한 변환 과정을 우리는 환원이라고 부릅니다.
이 비유에서 일상적인 집안일은 NP 문제(빠르게 완료할 수 있는 작업)이고, 집 짓기는 NP-Hard 문제(가장 힘든 일상적인 집안일만큼 어려운 작업)입니다.
핵심은 집을 짓는 빠른 방법(다항식 시간 알고리즘)을 찾을 수 있다면(NP-Hard 문제 해결), 그 방법을 사용하여 일상적인 집안일을 빠르게 완료할 수 있다는 것입니다(NP에서 어떤 문제든 해결할 수 있음). 그렇기 때문에 어떤 문제가 NP-Hard 문제라는 것을 증명하는 것이 중요한 이유는 그 문제가 적어도 우리가 빨리 풀 수 있는 가장 어려운 문제만큼 어렵다는 것을 보여주기 때문입니다.
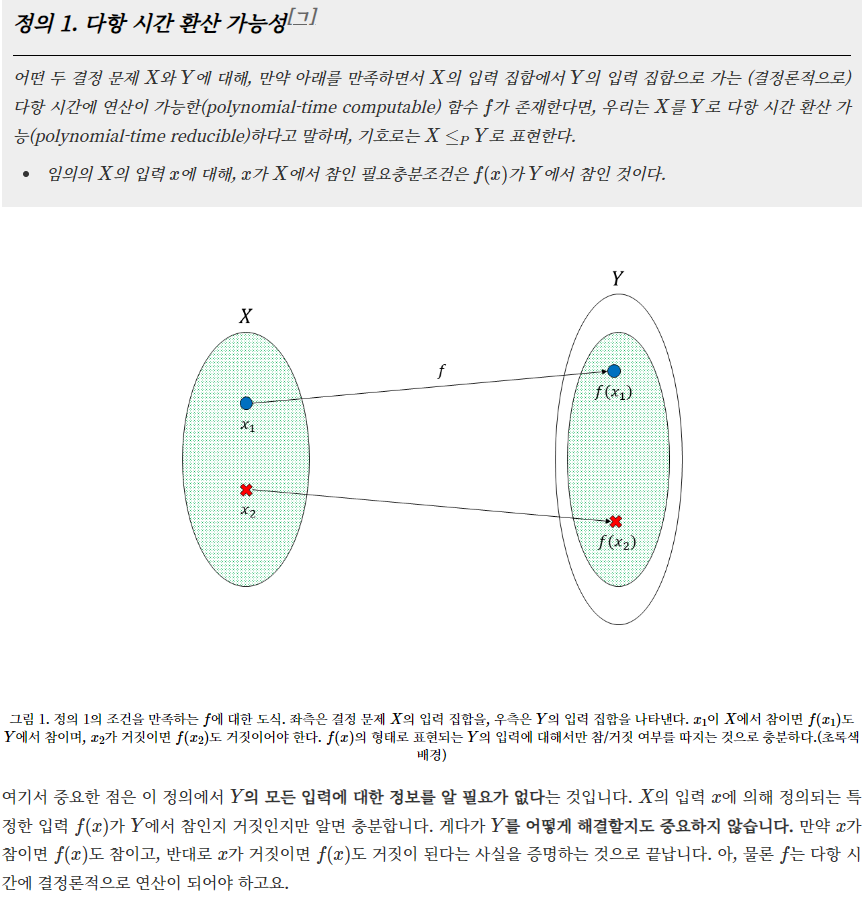
즉, 어떤 입력 x가 있는데, 이를 다항시간에 결정론적으로 연산이 되는 f에 넣은 f(x)로 만든 다음,
이 f(x)가 Y에서 참이기만 하면 x는 X에서 참이다.
이 때, 어떤 결정문제 Y가 NP에 속하면서 NP-Hard이면, Y는 NP-Complete.
정리하면

[증명] 정의에 의해 임의의 X∈NP에 대해 X≤pY이다. 따라서, 정의1의 조건을 만족하는 다항시간에 연산 가능한 함수 f가 존재. Y를 다항시간에 해결하는 알고리즘을 B라고 하자. 이때, 우리는 X를 다항시간에 결정론적으로 해결하는 알고리즘 A를 만들 수 있다. 어떻게? 임의의 입력 x에 대해, 먼저 f(x)를 계산 후, B에 f(x)를 넣어 결과를 얻는다. B가 참을 출력한다면, A도 따라서 참을 출력할 것이고, 거짓이라 하면 거짓을 반환할 것이다.
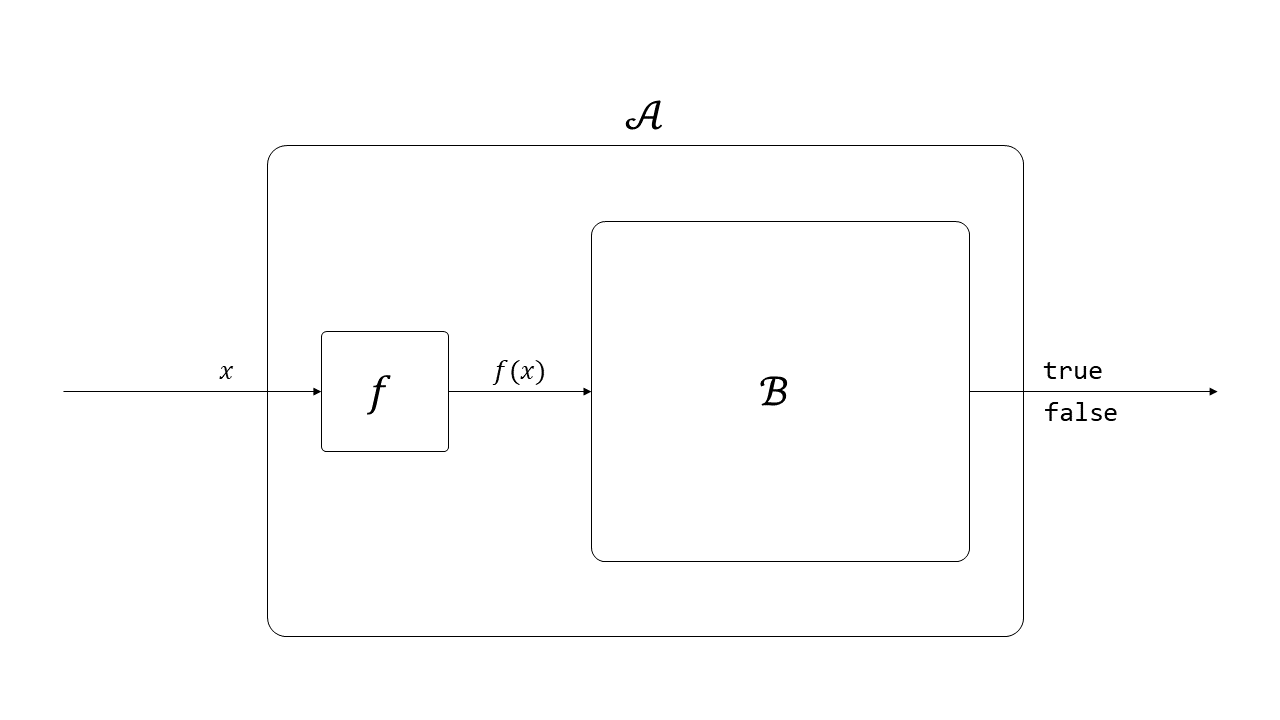
1) x가 X에서 참이라면, f의 성질에 의해 f(x)도 Y에서 참
1-2) B는 올바른 알고리즘이므로, f(x)가 입력으로 들어오면 참을 반환
1-3) 따라서 A도 참을 반환
2) x가 X에서 거짓이라면, f(x)는 Y에서 거짓
2-2) 따라서 B도 거짓을 반환
2-3) A도 거짓을 반화나
3) B, f 모두 다항시간에 결정론적으로 동작하므로, A도 다항시간에 결정론적으로 동작. 따라서 X∈P
4) 증명의 어떤 곳에서도 비결정론적 알고리즘에 의존하지 않음. 즉, 어떤 문제가 NP-Hard하다는 것은, 임의의 NP문제를 해당 문제로 다항시간에 환산해 해결할 수 있단 것만 나타냄. 다른 건 신경쓰지 않음.
추가적으로, 해당 문제를 비결정론적 알고리즘으로 다항시간에 해결할 수 있단 사실을 알면 이는 NP에 속하게 되고, 따라서 NP-Complete.
그럼 NP-Hard이면서 NP는 아닌 경우, 즉 NP-Complete가 아닌 경우는?
정지 문제 : 모순되는 프로그램. undeciable하기에, NP-Hard하지만 NP는 아님.
NP-Hard만큼 어렵지만, 다항식 시간 내에 해를 확인할 수는 없음.
[주말N수학] 절대로 해결할 수 없는 문제 : 동아사이언스 (dongascience.com)
[주말N수학] 절대로 해결할 수 없는 문제
앨런 튜링(1912-1954) 컴퓨터가 탄생하는 데 수학이 어떤 역할을 했을까. 영국의 수학자이자 현대 컴퓨터의 창시자인 앨런 튜링은 일종의 판정 문제인 ‘정지 문제’를 ‘튜링 기계’를 이용해 풀
m.dongascience.com
정지문제는 모든 인스턴스에 대한 실험이 불가하기에 NP-Hard이지만 NP는 아님.
정지 문제는 NP-hard이며, 이것은 정지 문제를 해결할 수 있는 다항식 시간 알고리즘이 있다면, 그 알고리즘이 NP의 모든 문제를 다항식 시간에 해결하는 데 사용될 수 있다는 것을 의미합니다. 이는 NP의 모든 문제가 다항 시간 내에 정지 문제로 축소될 수 있기 때문입니다.
다음은 이러한 절감 효과에 대한 대략적인 개요입니다:
1. NP에서 임의 문제의 인스턴스가 주어지면, 우리는 그 문제에 대한 가능한 모든 해결책을 시도하는 프로그램을 구성할 수 있습니다(문제가 NP에 있기 때문에, 우리는 어떤 해결책에 대한 다항식 시간 검증기가 있다는 것을 알고 있습니다).
2. 이 프로그램은 문제에 대한 해결책을 찾은 경우에만 중단됩니다.
3. 따라서 정지 문제를 해결할 수 있다면 원래 문제에 대한 해결책이 존재하는지 여부를 판단하는 데 사용할 수 있습니다.
그러나 정지 문제는 NP-hard이지만 NP(또는 co-NP)에는 없습니다. 이것은 정지 문제에 대한 솔루션에 대한 다항식 시간 검증기가 없고, 그 보완에 대한 다항식 시간 검증기도 없기 때문입니다. 사실 정지 문제는 재귀적으로 열거 가능하다고 알려진 더 큰 문제 클래스에도 속하지 않습니다. 왜냐하면 정지 문제의 모든 인스턴스를 나열하는 알고리즘이 "예" 대답을 가지고 있지 않기 때문입니다.
또한 NP이지만 NP-Hard가 아닌 경우는 해당 문제로 축소(reduce)가 불가한 경우.
소수인지 확인하는 문제는, 숫자가 주어지면 다항식 시간 내에 소수인지 확인이 가능하기에 NP이지만, 다항식 시간 내에 NP의 어떤문제도 이 문제로 환원할 수 없다.
그렇다면 문제를 환원할 수 없다는 뜻은? >>
예를 들어 그래프에 해밀턴 주기(각 정점을 정확히 한 번씩 방문하는 주기)가 있는지 여부를 결정하는 문제가 NP-Hard임을 보여주기 위해, 그래프에 특정 길이의 순회 세일즈맨 투어가 있는지 여부를 결정하는 알려진 NP-Hard 문제를 해밀턴 주기 문제로 축소할 수 있다.
여기에는 그래프와 길이 L이 주어졌을 때, 원래 그래프가 길이 L의 순회 세일즈맨 투어를 갖는 경우에만 새 그래프가 해밀턴 사이클을 갖도록 다항식 시간 내에 새 그래프를 구성할 수 있음을 보여주는 것이 포함된다.
'미연시리뷰' 카테고리의 다른 글
| [Optical flow] GMFlow (0) | 2023.10.16 |
|---|---|
| [통계 정리] 확통 사이트 및 개념 (0) | 2023.06.09 |
| [Diffusion] 참고용링크 (0) | 2023.04.24 |
| Optical Flow (2) | 2023.02.24 |
| [통계 정리] 통계와 확률 정리 & PRML 목차 (0) | 2023.02.13 |



