[논문] VAE(Auto-Encoding Variational Bayes) 직관적 이해 - Taeu
[논문] VAE(Auto-Encoding Variational Bayes) 직관적 이해
VAE : Variational Auto-Encoder를 직관적으로 이해하기!
taeu.github.io
Diffusion Model 입문하기 (velog.io)
Diffusion Model 입문하기
이 글은 딥러닝 감수성은 있지만 디퓨전 감수성이 부족한 사람들을 위해 쓰이는 글컴퓨터 비전 분야의 직관 기반 연구 논문은 잘 읽을 수 있는데, 디퓨전의 경우 이론이 너무 어려워서 어떻게
velog.io
[Paper Review] Denoising Diffusion Probabilistic Models - YouTube
팔자에도 없는 디퓨전을 공부하게 되었구나
KL과 (크로스)엔트로피
초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기 (hyunw.kim)
그림1


VAE와 Diffusion의 loss 차이점

Regularization과 Reconstruction은 VAE와 같으나,
Denoising process가 추가됨. 많은 수의 latent variable을 만들어가는 디퓨전 특성 상, 마르코프 체인과 관련된 위와 같은 프로세스가 추가됨.
최종적인 XT시점에서 X1까지 이어지는 디노이징 프로세스의 학습을 가이드하는 역할을 맡음.

이젠, 이 DDPM이 어떻게 접근해서 어떤 효과를 획득?

마치 MSE와 같은 loss임. Ground-Truth인 ε와, 학습대상인 εθ의 차이로 Loss가 구성.
각 t라는 시점의 노이즈인 θ를 모델이 예측하도록 하는 loss라 보면 편하다.
우선, 기존의 위의 논문에서 Regularization이 제거됨. 굳이 T시점의 Regularization을 이용해 βt를 학습하지 않더라도, T시점의 latent variable이 Istropic gauusian과 유사하다고 한다.

특정 범위에서 β를 linear scheduling을 통해 가져가게 되어 얻어낸 T시점의 latent variable은 isotropic한 가우시안을 따른다고 함.
loss term에서 regularization을 제외하고 noise크기인 β도 학습대상이 아닌 fixed schedule에 따른 값으로 고정.
다음으로 Denoising process를 재구성.

조건부 가우시안분포의 각 시전별 평균과 분산을 모델이 예측하도록 해야 한다고 앞서 말함.
그래서 학습대상 중, 분산을 제외하고 평균만 가져간다.

β는 이미 알고 있다. 정해진 스케쥴에 따라 노이즈가 추가되기에.
이 값을 이용해, 분산을 각 시점별 누적된 노이즈 크기로 상수화시킴.

기존의 Denosing process를 mean function 관점으로 변경시, 아래와 같아짐.
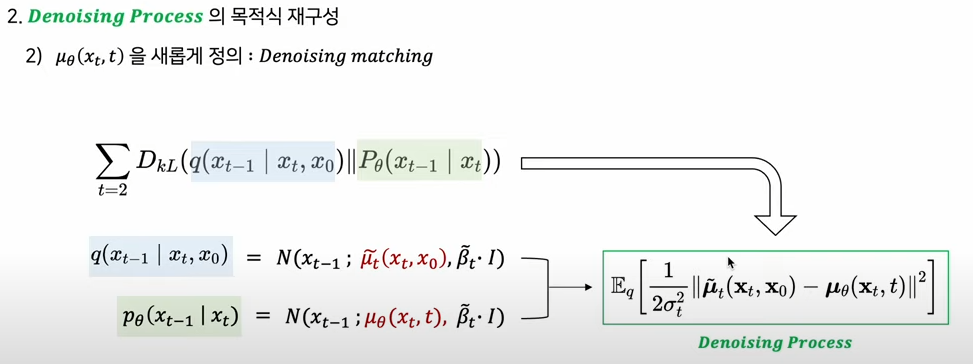
Denoising process loss term인 KL분산을 구성하는 P와 Q라는 분포를 mean function으로 학습대상인 모수로 정리할 수 있음.
둘 간의 kl-divergence는 mean-func간 차이로 정리할 수 있음(오른쪽의 상자).

학습대상인 mean func을 denoising이란 관점에서, 'denosing matching'으로 새로이 정의.
이를 위해, t시점의 x를 보이는 수식과 같이 표기(xt(x0, ε)).
t시점의 x는 diffusion process에서 x0로부터의 마르코프 체인을 반복해서 forward를 해나가면 획득이 가능한데,t번의 마르코프체인을 거쳐 얻어낸 xt가 곧 위의 첫 문장처럼 표기됨.
xt수식의 각 항목에서, 첫 번째 텀의 α : 1-β : (1 - 노이즈 크기). 이미 알고 있는 정보. x0 : 디퓨전 프로세스상에서 이미 알고 있는 정보.
두 번째 텀의 1 - α : 이미 알고 있음.즉, 학습해야 하는 것은 ε뿐.
이 상태에서, 이 xt를 수식(1)에 대입 시, 수식(2)와 같이 정리가 됨.

이 수식(1)을 다시 보면, 수식(2)의 mean function이 학습해야 할 것은 t시점의 붉은 underline.
이 붉은 곳에서 알지 못하는 것은 ε뿐이라 했다.
이 ε에 θ를 부여해서 (2)를 재정의하면 (3)과 같아짐.

(2)와 (3)을 조합하면 (4)가 나오며,
이 (4)는 ε에 대한 MSE 구성에, 노이즈로 조합된 계수 term이 붙어있는 형태.
이를 더욱 간소화한 것이 아래.

결국 최종적 Loss는 아래와 같아짐.

간소화된 loss를 noise estimation 형태로 나타냄. 이것이 왜 denoising인지 나타냄.
'미연시리뷰' 카테고리의 다른 글
| [통계 정리] 확통 사이트 및 개념 (0) | 2023.06.09 |
|---|---|
| [알고리즘] P & NP (0) | 2023.06.08 |
| Optical Flow (2) | 2023.02.24 |
| [통계 정리] 통계와 확률 정리 & PRML 목차 (0) | 2023.02.13 |
| 캐글 (0) | 2021.08.23 |



