동적 비전은, 2차원 영상 공간에 시간축이 더해진 것. 즉 f(y,x,t)는, t라는 순가의 (y,x)화소의 명암값.
동적비전은, 장면에 담긴 물체에 대한 정보를 알아내는 것이 목표. 이엔 물체의 부류, 움직이는 속도와 방향, 물체가 하는 일에 관한 행위인식이다. (실시간 3차원 장면 재구성해 시청자에게 전달하는 시범시스템 ohta2007, 서버컴퓨터에 실시간 영상 보내면 이를 분석해 3차원으로 재구성한 후 TV로 전송)
동적비전에 대한 연구 난이도는
물체의 3차원 모양과 움직임 재구성(3차원 스포츠 중계) - 장면 이해(항해로봇, 자율주행 자동차) - 비디오 검색(방송 콘텐츠 관리) - 물체동작 인식(게임, 감시) - 물체 추적(감시) - 물체 개수 파악(교통량, 인파 측정 혹은 현미경 영상의 세균 밀도 측정) - 움직이는 물체 존재 여부 인식(현관, 지하 주차장의 자동소등 장치)순으로 어렵다.
입력 : 연속영상 f(x,t)
출력 : f에서 추출한 움직임 정보
for t=1 to T:
f(x,t)를 처리해 특징집합 m_t 추출
T개의 특징집합에서 움직임 정보 생성영상은 공간 일관성을 가지며, 즉 어떤 화소가 특정 색을 가졌다면 주변ㄴ 화소도 유사한 색을 가질 가능성이 높다. 에지 추출, 영상 분할, 지역특징 추출은 이를 활용한 사례. 여기에, 시간 일관성이 포함됨으로써, f(y,x,t)는 f(y,x,t+1)과 비슷할 가능성이 있다. 이 두 일관성을 고려하는게 중요.
차 영상 : jain81
r이라는 순간과 t라는 순간의 차 영상을 정의한다. 때로 r은 t-1 또는 t-n과 같은 이전 프레임일 수 있고, 아닐 수도 있다.
d_tr(y,x) = abs(f(y,x,t) - f(y,x,r)) > tau ? 1 : 0아래는 차 영상을 사용해 움직임 정보를 알아냄. 기준 프레임 r은 응용상황에 맞게 설정하며,
마지막 행은 연결요소를 해석해 움직임 정보를 추출한다.
cctv같은 감시가 목적이라면, 일정크기 이상의 연결요소가 발견되면 침입자가 있다고 간주하듯.
입력 : 두 장의 영상 f(x,r) & f(x,t)
출력 : 움직임 정보
차 영상 d를 구함 (by 위의 식이나 아래 식)
d의 연결요소 구함
크기 작은 연결요소 제거 #잡음으로 간주
적절한 모폴로지 연산 수행 #가령 열기 연산
연결요소 해석해 움직임정보 추출차 영상을 구하는 또다른 수식 아래는, 화소의 주위를 살피고 변화가 있는지 여부를 판단.
이 식에서 μ_t과 σ_t는 영상 t의 (y,x) 화소에 씌운 m*n크기 윈도우 내의 화소 평균과 분산.
차 영상은 화소를 개별적으로 처리하므로 잡임에 민감하다.
d_tr(y,x) = 1/(σ_t * σ_r) * pow((σ_t + σ_r) / 2 + pow((μ_t - μ_r)/2, 2), 2) > τ ? 1 : 0자세한 예시는 책.
모션 필드: 연속된 두 장의 영상 f_t와 f_(t+1)로부터 2차원 상이 모션벡터 or 속도벡터라 부르는 v 알아내는 법
--> 움직임이 발생한 모든 점의 모션벡터를 알아내면, 2차원 모션 맵이 얻어진다. 이것이 모션필드
이러한 모션 필드의 추정이 가능하면 목표물추적이나 제스처인식 등이 가능.
그러나 구가 회전하는 상황에선 모션벡터는 발생하지만 영상엔 변화가 없다. 이 과정에서 해가 움직인다면 모션벡터는 0어야 하나 변화 자체는 발생하므로, 알고리즘은 0이 아닌 모션벡터를 추정할 것(horn86, 12.1)
광류
인접한 두 영상의 명암변화만 고려. 광류 알고리즘이 추정해야할 모션벡터는 v=(v,u), 이 떄 v와 u는 각각 y와 x방향의 이동량.
인접한 두 영상의 시간차 dt가 충분히 작다면, 테일러급수에 따라 아래 식이 성립. 이 때, 초당 30프레임라면 dt = 1/30초.
f(y+dy, x+dx, t+dt) = f(y,x,t) + Δf/Δy * dy + Δf/Δx * dx + Δf/Δt * dt + 2차 이상의 항dt라는 시간동안 (dy,dx)만큼 움직여 형성된 새로운 점은 원래 점의 f(y,x,t)와 같다(by 밝기 항상성).
따라서 위의 식은 Δf/Δy * dy + Δf/Δx * dx + Δf/Δt * dt = 0 을 통해, 양변을 dt로 나누면
Δf/Δy * dy/dt + Δf/Δx * dx/dt + Δf/Δt = 0를 획득가능. 이 때, Δf/Δy와 Δf/Δx, Δf/Δt는 각각 영상 f(y,x,t)를 매개변수 미분한 편도함수로, 그레디언트 (Δf/Δy, Δy/Δx)는 3장의 에지거물에 사용한 식과 같다.
dy/dt와 dx/dt는 시간 dt동안의 y와 x방향으로의 이동량이므로, 모션벡터에 해당한다. 즉 각각 v와 u에 해당한다. 즉
Δf/Δy * v + Δf/Δx * u + Δf/Δt = 0가 우도됨. 이것이 광류조건식, 그레디언트 조건식
lucas-kanade와 horn-schunck알고리즘이 이를 이용한다.
물론 그레디언트 구성하는 세 개의 값들을 다 구해도, v와 u를 유일한 값으로 결정할 수 없다. 방정식은 하나인데 구해야 할 값은 v와 u 2개니까.
광류조건식에 대한 예제는 책 참조.
광류 추정 알고리즘 : lucas-kanade와 horn-schunck
루카스 카나데(lucas81,84)는 지역적 방법으로, 화소 (y,x)를 중심으로 하는 윈도우영역 N(y,x)의 광류는 같다고 가정.
즉 이웃화소는 같은 모션벡터 (v,u)를 갖는 것이다. 이 때 n은 영역 N(,)에 속하는 화소의 개수며, 각 화소는 모두 상술한 광류조건식을 만족한다.
전제조건 3가지 밝기 향상성 (brightness constancy), Frame 간 움직임이 작다, 픽셀 (y,x)를 중심으로 하는 윈도우 영역 N(y,x)의 optical flow는 같다는 것이 만족된다고 가정하면, 이 경우에
Δf(y_i, x_i) / Δ(y) * v + Δf(y_i, x_i) / Δ(x) * u + Δf(y_i, x_i) / Δ(t) = 0,
이 때 (y_i, x_i)는 N(y,x) 내 원소이며, 미지수는 v와 u 두개지만, 식은 n개가 된다. 따라소 최소제곱법으로 미지수 구하는 것이 가능.
Av^t = b
이 때 A =
[[Δf(y_1, x_1) / Δy, Δf(y_1, x_1) / Δx], ... [Δf(y_n, x_n) / Δy, Δf(y_n, x_n) / Δx]]
v = (v, u)
b = [-Δf(y_1, x_1) / Δt, ...., Δf(y_n, x_n) / Δt]위 식을 정리하면
A^TAV^T = A^Tb를 통해,
v^T = (A^TA)^(-1)A^Tb
를 얻을 수 있다.
우변의 첫번째 항은 (A^TA)^(-1)에 해당하는 2*2행렬, 두번째 항은 A^Tb에 해당하는 2*1행렬.
첫번째 항은 Δt를 포함하지 않기에, t순간의 영상만 있으면 모든 계산이 가능.
두번쨰 항은 t순간과 t+1순가의 영상을 다 사용하기에, 이 식을 풀면 모션벡터 얻는 것이 가능.

위 식은 윈도우 영역 N(.)에 속한 모든 픽셀을 같은 비중으로 취급하는데, 윈도우의 중앙화소 (y,x)에 가까울수록 큰 비중을 두는 가우시안 식으로 바꾸면 더 나은 품질의 모션벡터 획득이 가능.
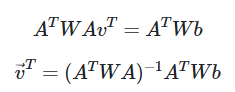
풀어쓰면 아래와 같다.
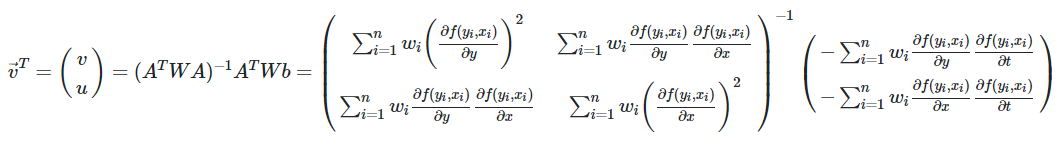
아래의 알고리즘에서 repeat은 위의 식을 반복하는 것이다. 이 때 새로 계산한 (v,u) 크기가 임계값보다 작으면, 수렴했다 간주하고 반복을 멈춘다.
(v,u)는 실수이고 모든 화소 좌표는 정수이기에, 보간을 적용해 얻은 화소값을 사용한다. 2.4절의 선형보간이나 3차보간을 사용한다.
이 알고리즘은 각 화소에서 계싼한 도함수값을 바탕으로 광류를 구하므로, 어떤 물체의 표면에 명암변화가 나타나지 않으면 도함수값이 0이 되어, 해당 영역의 광류가 0이 된다는 문제가 있다.
입력 : 인접한 두 장의 영상, 임계값 e
출력 : 광류맵 v(y,x), 0<=y<=M-1, 0<=x<=N-1
for y=0 to M-1:
for x=0 to N-1:
v(y,x) = velocity_vector(y, x, f_t, f_(t+1)) #두 장의 입력 영상 f
func velocity_vector(y, x, f_t, f_(t+1)) :
if (y,x)에 씌운 윈도우가 영상 안 벗어나면 :
cy, cx = y, x
do {
식을 이용, 화소 (cy, cx)의 모션벡터 (v,u) 계산
cy, cx = cy+v, cx+u
} while (||(v,u)|| < e)
ret ((cy-y, cx-x)) #추정된 모션벡터
else :
ret (Nil) #광류계산 불가https://gaussian37.github.io/vision-concept-optical_flow/#
옵티컬 플로우 (Optical Flow) 알아보기 (Luckas-Kanade w/ Pyramid, Horn-Schunck, FlowNet 등)
gaussian37's blog
gaussian37.github.io
이러한 알고리즘은, 물체의 표면이 평면이면 표면 내부의 명암변화가 적게 나타나기에, 내부 광류는 0이고 경계 부분만 광류가 발생하여, 경계 부근만 같은 모션벡터를 가져 속이 빈 직육면체 등으로 직육면체를 판단할 수 있다.
또한 이는 지역적 알고리즘이기에, 큰 윈도우를 쓰면 큰 움직임을 알아낼 수 있지만 넓은 영역을 스무딩하기에, 모션벡터 정확도가 떨어진다.
이는 피라미드기법을 활용해(bouguet2000) 어느정도 선에서 광류의 정확도 희생 않고 움직임을 낮은 해상도에서 알아내는 것이 가능.
Horn-Schunck 알고리즘: 영상 전체를 한꺼번에 고려(horn81, 86)
광류는 부드러워야 한다는 가정을 토대로, 이 광류맵의 부드러운 정도는 아래를 통해 측정.
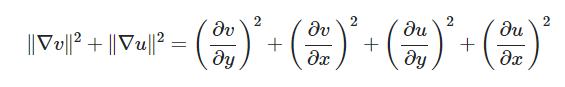
v를 y와 x방향으로 미분한 그레디언트로, 이들 그레디언트가 작다는 말은 이웃한 화소의 v와 u가 비슷하다는 뜻.
또한, 해당 알고리즘은 앞서 말했던 광류조건식(이하)도 만족해야 한다.
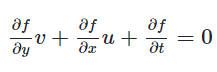
따라서, 해당 식을 0에 가깝게 함과 동시에, 위의 식을 값을 될수 있는 한 작게 하는 해를 찾아야 한다.
해당 알고리즘은 영상 전체에 대해 이들 값을 최소로 하는 해를 찾는 것을 전략으로 삼으며, 이러한 전략을 반영한 것이 아래의 식이다. 적분식 속의 첫 항과 두번째 항은 앞서 설명한 바 있으며, alpha는 어느 것에 큰 비중을 둘 지 정하는 가중치이다. 이를 크게 할수록, 광류맵이 더 부드러워진다.
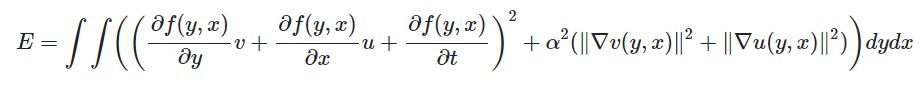
이제 해당 식을 최소로 하는 광류맵, 즉 모든 화소 (y,x)에 대한 v(y,x) = (v(y,x), u(y,x))를 구하는 것은 아래의 반복식으로 계사난다.
pow(v, k+1)은 k+1번 반복해 얻느 값이며, 초기값 v^0은 0이다. pow(v, -k)는 현 화소를 중심으로 하는 윈도우의 평균이다. 수식유도 과정이나 도함수 계산법, pow(v(u), -k)의 계산법이나 alpha값 설정에 대해선 Horn81 참고.
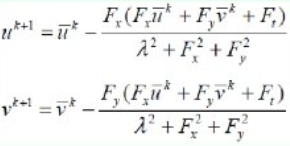
이를 알고리즘으로 표현하면 아래와 같다.
기타 광류 추정 알고리즘: LK가 지역적, HS가 전역적이므로, LK는 광류값이 정해지지 않는 영역에 군데군데 발생할 수 있는데, 특히 명암변화가 적은 곳에서 심하다. 반대로 HS는 반복과정에서 명암변화가 적은 영역에도 정보가 파급되기에, 모든 화소가 모션벡터를 갖는 밀접된 광류맵을 생성한다.
Bruhn2005는 두 알고리즘의 장점을 결합한다.
HS는 제곱항으로 정의되는 식을 사용하기에, 물체경계에 해당하는 불연속점이 불분형해지는 단점이 있으며, 이를 절댓값항을 이용해 성능을 높일 수 있다(ZACH2007).
입력: 두 인접한 영상, 임계값 e
출력: 광류맵 v(y,x), 0<=y<=M-1, 0<=x<=N-1
for(모든화소 (y,x)) v_0(y,x) = 0 #첫값을 0으로 초기화
k=0
do :
v_(k+1) 구하기
오류 E 계산
k++
while (E<e)
위의 것은 다 미분을 사용하는데, 그 외 미분방법에 대한 소개는 FLEET2005를, 미분방법 외의 것은 BARRON94를 보면 된다.
MRF방식을 이용한 LI2009(3.5), GLOCKER2008, HEITZ93, 여러 알고리즘으로 얻은 광류를 그래프절단 알고리즘으로 결합하는 Lempitsky2008, 광류추정과정에서 사용하는 필터를 학습을 통해 설게하는 학습기반 방법 sun2008도 있으며, baker2007은 이것들의 성능비교실험을 보여준다.
광류의 활용: 광류맵은 물체 추적, 인식 등의 중간표현이다. 물체가 어떤 곳으로 이동함과 동시에 카메라가 가까워질 때 모션벡터가 모이는 점이 확장중심점(FOE)로 부르는데, 이러한 FOE추정 알고리즘은 tistarelli91가 있다.
광류를 이용해 여러 문제를 푸는 o'donovan2005가 있으며, 이를 이용해 인식을 수행한 사례는 cedras95가 있다. 가령 독화술은 입술의 움직임을 분석해 무슨 말인지 인식하는 것이다. shaikh2010은 입술영상에서 광류를 추정, 광류맵에서 특징벡터를 추출해 svm으로 분류를 시도한 것이며, 광류학습기반방법인 sun2008로 추출했다.
물체 추적
광류맵은 물체의 움직임을 나타내는 궤적의 정보를 지니고 있지만, 명시적이지 않고 암시적이다.
즉 물체의 움직임 추적엔, 광류맵에서 궤적을 나타내는 특징을 추출해 궤적 정보로 변환하는 과정이 필요하다.
이를 위해, 첫 프레임에서 관심있는 물체 검출 -> 연속 영상에서 움직임 궤적 추적 -> 여러 물체를 동시에 추적 등을 해야 한다. yilmaz2006에서 자세하게 볼 수 있다.
KLT 추적 알고리즘: Tomasi91, shi94에 소개되어 있으며, 상술한 d_tr을 구하는 알고리즘에서 더 나아간다.
우선, 추적에 유리한 특징점을 구하는 것이다. 상술한 광류추정 알고리즘의 A^TA행렬은 Δf/Δy와 Δf/Δx만 지니고 있기에, 다음 프레임과 무관하게 현 프레임 f(y,x,t)에서 모든 요소의 계산이 가능하다.
해당 행렬에서 y,x방향 모두 변화가 없는 지점은 H=2*2크기의 0행렬이 되기에, 모션벡터가 0이 되며, 즉 변화가 있어도 약한 지점은 작은 잡음에 큰 영향을 받기에 믿을만한 모션벡터가 되진 못한다. 즉 이런 지점을 배제, 추적에 유리한 안정적 특징점 찾아내는 규칙이 필요하다. 즉 H(=A^TA)의 두 고유값 중 작은 것의 크기가 임계값 λ
min(λ_1, λ_2) > λ보다 크면, 그 점을 추적에 적절한 특징으로 취한다.
두 고유값이 작은 지점은 명암 변화가 거의 없는 곳으로, 하나만 큰 곳은 한 방향으로면 변화가 있는 곳이다. 즉 에지일 가능성이 크다. 둘 다 크다면, 여러 방향으로 변화가 있는 지점으로, 다음 프레임에서도 이 점을 찾기 쉬워 추적에 유리하다.
해당 방식에서 기반을 둬, 우선 1행에선 첫 프레임 f_1에서 추적 대상이 되는 특징점을 검출한다. 이 때 해당 λ 비교식을 만족하는 점은 특정 영역에 밀집되어 나타날 수 있기에, 비최대 억제같은 방식으로 적절하게 골라내야 한다. tomasi91에선 비최대억제 대신, 특징점을 min(λ_1, λ_2)로 정렬한 후 큰 값을 갖는 점부터 취하는데, 이미 취한 점과 일정 거리 안에 있는 것은 배제하는 바익을 썼다.
추적대상이 되는 특징점 검출 후엔, 두 번째부턴 그들을 추적한다. 이 때, velocity_vector()을 재활용한다.
광류를 물체 추적에 쓰는 데의 두 가지 사항은, 우선 최초 프레임에서 추적 대상이 되는 특징점을 골라내는 것, 두 번째는 추적 도중 특징점이 영상 밖으로 벗어나거나 다른 물체를 가리거나 멀어져 실종되는 것인데, 첫 번째는 1행이다. 두 번쨰는 5행에 해당한다.
실종여부를 판단하는 것은 min(λ...)식으로 판단할 수 있으며, shi94는 어파인 변환에 필요한 매개변수와 이동에 필요한 매개변수를 포함한 모델로, 5행에서 해당 모델을 이용해 실종여부 판정, 그 실종된 특징점을 삭제하는 알고리즘을 설명한다.
입력: 연속영상 f_t(y,x), 0<=y<=M-1, 0<=x<=N-1, 1<=t<=T
출력: p_t(i), 1<=i<=n, 1<=t<=T
f_1에서 min식에 해당하는 점을 찾고, 그중 특지점을 골라내 p1(i), i=1,2,...n에 저장한다
for t=1 to T-1:
for i=1 to n:
p_(t+1) = velicity_vector(p_t(i).v, p_t(i).u, f_t, f_(t+1))
p_(t+1)의 실종여부 판정 후, 실종시 p_(t+1) = Nil로 설정해 추적을 포기
큰 이동 추적: 광류 맵 추적 알고리즘은, 큰 이동이 일어나는 영역에선 모션벡터를 제대로 추정하지 못한다. 이러한 해결법은 두 가지가 있다.
연속 영상의 두 인접한 영상을, 대응점을 찾은 후 대응점을 잇는 벡터를 모션 벡터로 취하면 된다.
그러나 대응점은 희소하므로, 보간을 통해 밀집된 광류맵으로 표현해야 하는데, 이에서 큰 오류가 발생할 수 있다.
또한 대응점 리스트에 아웃라이어가 포함될 수 있다.
이는, 댕으점찾기를 통해 희소한 모션 벡터 생성 후, Horn-schunck알고리즘을 적용하면 된다(brox2009(2011)).
weinzaepfel2013도 비슷한 접근을 취하는데, sift기술자를 이용한다. 기존 sift는 경직된 16개 블록을 사용하지만, 이는 4*4 격자를 2*2짜리 4개로 나누고 이들이 일정 거리 내에서 분리될 수 있게 허용해 대응점을 보다 정확하게 알아내는데, 이를 이용한 깊은 신경망은 Weinzaepfel2013을 참조하면 좋다.
'버츄얼유튜버' 카테고리의 다른 글
| 바보♡ 허접♡ 코하루도 이해하는 욜로(YOLO) (2) | 2022.01.29 |
|---|---|
| Pandas (0) | 2022.01.20 |
| 비전 9 ) 인식 (0) | 2022.01.08 |
| 비전 8) 기계학습 (0) | 2021.12.31 |
| 비전7 ) 매칭 (0) | 2021.12.29 |

