
해당 과정에서 sigmoid의 단점을 파악 가능.
1) sigmoid 함수의 미분은 x(1-x)인데, [0,1]에서 최대값은 1/4임.
만일 충분히 작은 값이 sigmoid에 들어오게 된다면 이는 0에 가까운 값을 출력.
그럼 backpropagation 과정에서, sigmoid 특성 상 미분값(x-(1-x))도 0에 가까운 출력을 내보이게 됨.
즉, 이것이 곱해질 dE/dW가 0에 한없이 비슷한 값이라는 것.
2) 또한 sigmoid는 가운데값이 0이 아닌, 0.5다.
즉 출력이 무조건 [0,1]으로, 양수이다. 따라서 w에 대한 미분은 무조건 양수가 된다.
왜? 위 사진의, 오른쪽 상단 부분의 dz/dw를 살펴보라.
Chain Rule 적용 과정에서 dz3/dw5 = h1임을 알 수 있다.
가중치*입력을 가중치로 미분하면, 그 결과는 입력일 수밖에 없고, 그 입력은 곧 이전 노드의 활성화함수(여기에선 시그모이드)의 출력일 수밖에 없다.
즉, local gradient(dz/dw와 같은, 자기 옆의 녀석과 미분하는 국소적미분)의 결과는 무조건 양수다.
이를 통해, 가중치는 무조건 다 더해지거나 다 빼지는 결과를 갖게 되며,
당연히 필요에 따라 하나의 가중치는 더해지고 하나의 가중치는 빼져야 하기에 매우 번거롭게 된다.
TanH : [-1,1] 으로 2의 문제를 해결하지만, 1의 문제를 해결하지 못함
ReLU: f(x) = max(0,x) 로, 양수에서는 1의 문제가 해결됨. 또한 exp 계산이 없어 빠름. 그러나 2를 해결하지 못하고, 입력값이 음수라면, gradient가 다 죽어버린다. 0이 나오므로, 학습이 전혀 안 되고 backpropagation이 0이 전달됨.
leaky ReLU: max(0.1x, x) 로, x가 음수인 영역 값에 대해 미분값이 0이 되지 않는단 점을 제외하면 ReLU와 동일하다. 양수와 음수 동시에 1의 문제를 해결한다.
PReLU: 추가 alpha를 max(α*x, x)로 넣음으로써 음수 영역에서의 미분이 가능케 한다.
ELU :

x가 0이하일 때 f(x)값이 0이 아니라 음수값으로 부드럽게 이어지며,
x가 음수에서 아무리 커져도 -1(에 의해 -1외에 조절 가능)의 일정한 음수값에 수렴하므로 노이즈에 덜 민감하다.
또한 x가 음수일 때의 기울기가 exponential로 부드럽게 감소하며,
x가 음수로 아무리 커져도 기울기는 0으로 수렴하므로 역시 노이즈에 덜 민감하다.
Maxout 뉴런 :

뉴런당 파라미터가 2배가 된다. W1와 W2를 지니고 있어야 됨.
위에서 보면 알겠지만, 입력 데이터를 Zero-mean으로 전처리하는 것은 중요하다.
이러한 zero-mean을 한 다음에는 normalization을 하는데,
이러한 과정들을 통해, 모든 차원이 동일한 범위 안에 있게 함으로써, 동등한 기여를 하게 하는 것.
이미지의 경우는 실제로 이미 각 차원 간에 스케일이 어느 정도 맞춰져 있기에, zero-centering만 실행하고 정규화는 안 함.
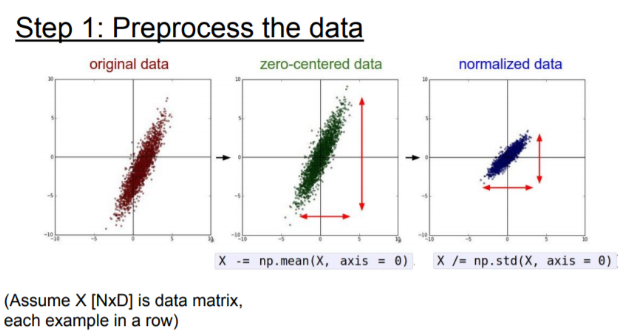
간단히 표현하면 위와 같다. zero-centering을 통해 각 데이터들을 중심으로 옮기고, 정규화를 통해 모든 데이터가 0~1의 값을 갖게 함으로써 명확한 기준으로 볼 수 있게 한다.
근데 위에서 sigmoid가 zero-mean이 필요하다 했다!
데이터 전처리는 sigmoid의 zero-mean문제를 오직 첫 번째 레이어에서만 해결할 수 있고, 다음 레이어에선 다시 문제가 불거진다. sigmoid의 문제점이 또 여기에서 나타난다.
PCA(데이터를 정규화시키고 공분산행렬 만들기)를 통해서도 압축이 가능하다.
SVD Factorization의 생성이 가능해지는데,
# U : 고유벡터, 정규직교 벡터 = basis vector.
# 이 U행렬의 column 벡터는, 각 벡터에 상응하는 eigenvalue의 내림차순으로 정렬됨
# S : 특이값의 1차원 배열
U, S, V = np.linalg.svd(cov)x를 고유기저(eigenbasis)로 사상(projection)시킴으로써 데이터 간의 상관관계 제거가 가능하다.
Xrot = np.dot(X, U)
Xrot_redued = np.do(X, U[:, :100]) # Xrot_reduced -> [N X 100]이 결과를 통해 [N X 100] 크기의 데이터로 아북되며, 데이터의 분산이 가능한 큰 값을 갖도록 하는 100개의 차원이 선택된다.
가중치 초기화: 0으로 초기화하면, 역전파 과정에서 미분값이 동일하다. 따라서 안 된다.
하비에르 초기화 : 노드가 n개일 때, 초깃값의 표준편차가 1/sqrt(n)이 되도록 가중치 설정.
ReLU같은 비선형에서는, 음수인 경우 가중치가 모두 0이기에, 기울기도 반토막이 된다.
He 초기화 : 노드가 n개일 때, 표준편차가 sqrt(1/n)이 되도록 가중치 설정. ReLU에 적합.
배치 정규화: 각 층에서의 활성화 값을 적당히 분포시킴으로써, 학습의 속도 증가, 초기값 의존성 감소, 오버피팅 억제
어파인(행렬곱) - 배치정규화 - 활성화함수 로, 활성화함수 전에 삽입하여 활성화함수의 input을 평균을 0, 분산을 1로 생성.
배치 정규화(Batch Normalization)
gaussian37's blog
gaussian37.github.io
- 학습 단계에서 모든 Feature에 정규화를 해주게 되면 정규화로 인하여 Feature가 동일한 Scale이 되어 learning rate 결정에 유리해집니다.
- 왜냐하면 Feature의 Scale이 다르면 gradient descent를 하였을 때, gradient가 다르게 되고 같은 learning rate에 대하여 weight마다 반응하는 정도가 달라지게 됩니다.
- 하지만 정규화를 해주면 gradient descent에 따른 weight의 반응이 같아지기 때문에 학습에 유리해집니다.
- batch normalization을 적용하면 weight의 값이 평균이 0, 분산이 1인 상태로 분포가 되어지는데, 이 상태에서 ReLU가 activation으로 적용되면 전체 분포에서 음수에 해당하는 (1/2 비율) 부분이 0이 되어버립니다. 기껏 정규화를 했는데 의미가 없어져 버리게 됩니다.
- 따라서 γ,β가 정규화 값에 곱해지고 더해져서 ReLU가 적용되더라도 기존의 음수 부분이 모두 0으로 되지 않도록 방지해 주고 있습니다. 물론 이 값은 학습을 통해서 효율적인 결과를 내기 위한 값으로 찾아갑니다.
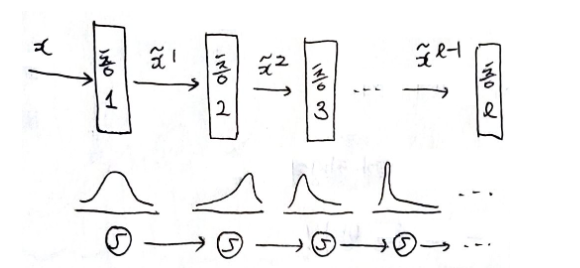
예를 들어, 학습을 하면서 계속해서 w의 값이 분포가 바뀐다고 가정하자. 어느 순간에서는 3~97을 갖더니,
학습을 하고 나니 -60~4의 값을 갖게 되는 것이다. 이처럼 학습 중간에 가중치가 계속 업데이트 되면서 학습 데이터의 분포가 수시로 바뀐다면, 학습이 잘 되지 않는다.
가중치 초기화를 하는 이유는, 각 층에서의 활성화 값이 고르게 분포되어야 하기 때문이다.
활성화 값이 한 쪽으로 치우친다는 것은 다수의 노드들이 같은 값을 출력한다는 의미이므로, 노드 여러 개를 둔 의미가 없다는 것이므로, 표현력이 제한된다는 뜻이다.
그러므로, 지금까지 본 공변량 시프트의 결과는 활성화 값이 고르게 분포되지 않는 것이라고 말할 수 있다.
따라서 위와 같은 과정을 통해, 인풋의 값을 적절하여 학습의 시간을 줄이고, learning rate의 조절 역시 가능하게 한다.
하이퍼파라미터 조정
https://say-young.tistory.com/entry/CS231n-Lecture-7-Optimizer?category=923651
CS231n - Lecture 7 (Optimizer)
CS231n Lecture7 - Training Neural NetworksⅡ의 전반부를 듣고 직접 제작한 PPT 자료입니다. 오류를 발견하시면 댓글로 말씀해주세요! (제가 발표를 담당한 주의 필기는 발표 대본으로 작성하기 때문에 다
say-young.tistory.com
SGD: 일부, 미니배치 1개만 갖고 학습을 진행하겠다. Good한 결과가 나오면, 나머지에도 적용한다.
왜 쓰는가? ) 평범한 Gradient Descent는, 모든 데이터를 사용해 학습하기 때문에 너무 시간이 오래걸리고 용량도 잡아먹는다. 따라서 SGD를 통해 용량을 줄일 수 있다.
단점 1) 즉석에서 기울기를 정해 그곳으로 움직이기 때문에 즉흥적이다. 즉, 최종적으로 큰수의 법칙에 의해 좋은 결과에 다다르긴 할 것인데, 여기엔 필연적으로 시간이 요구된다.
단점 2) Local minima에서의 탈출이 어렵다. 이러한 단점은 다른 기법에서도 부각되는 단점.
단점 3) mini-batch를 사용하기 때문에 step마다 정확한 gradient를 담을 수 없다. 일부 data를 추출해서 학습을 진행하는 것이기 때문에, gradient를 측정할 때 noise가 있으면 SGD가 최소값에 도달하는데 더 오래 걸릴 수도 있다.
이의 해결을 위해, Gradient=0일 때도, 멈추지 않게 하는 것이 필요하다.
사전에 알아둘 것은, SGD에서는 x = x + lr*dx

1) Momentum : 관성을 이용, 기울기가 오직 속도(velocity)에만 직접적으로 영향을 주고, 그 속도가 위치값(position)에 영향을 주게 됨. 이를 통해, 파라미터 벡터가 업데이트 되는 속도의 방향은 그라디언트들이 많이 향하는 방향으로 축적됨.
vx가 velocity, rho는 마찰계수(0.9~0.99)로, vx에 어느 정도 마찰을 주는 것이다. 이를 통해 gradient vector 방향 그대로 가는 것이 아니라, velocity vector의 방향으로 나아가게 됨.
코드를 보면, 맨 처음엔 vx0=0일 테니 while문 첫번째 기준 vx1=dx1이지만(즉 SGD랑 같지만),
이후에는 vx2=(dx1*0.9)+dx2=(vx1*0.9)+dx2,
vx3=0.9*((dx1*0.9)+dx2)+dx3=(vx2*0.9)+dx3,.... 으로 내려가는 건 미친듯이 빨리 내려가며(이전 dx가 vx가 되어 다음 것에 합쳐지니까), 설령 dx=0이 되더라도 이전의 vx가 여전히 살아있으니 어느 정도 다시 올라가는, 그야말로 관성에 가깝다고 할 수 있다. 다음 극점을 못 벗어난다면, 공이 골짜기에 빠져 올라갔다 내려갔다를 반복하다가 멈추는 것과 같은 효과를 내리라 추측 가능.

2) Nesterov Momentum : Error correcting이 추가되어, 이전 velocity와 현재 velocity의 차이를 반영한다.
현재의 속도 벡터와, 현재 속도로 한 걸음 미리 가 본 위치의 gradient vector을 더해 다음 위치를 정한다.
다음 속도 v_(t+1)은, 현재 속도에 마찰계수를 곱한 뒤, 한 걸음 미리 가본 위치의 그레디언트를 빼서 계산한다.
식을 보면 알 수 있는데, v_(t+1) = pv_t - lr*df(xt+pv_t) 에서
이 df(xt+pv_t)가 곧 현재 xt에서 p*v_t, 즉 현재 속도만큼 더 갔을 때의 미분(d)을 의미하기 때문이다.
이렇게 현재속도에서 다음속도를 빼는 과정을 반복하면, 이전의 모멘텀처럼 관성에 의해 과도하게 빨라지는 일을 방지할 수 있다.
3) AdaGrad : 각각의 매개변수에 맞게 매개변수를 조정.

이 매개변수인 학습률(lr)을, 기울기 제곱에 반비례하도록 조정하는데, 이를 통해 기울기가 가파를수록 조금 이동, 완만할수록 더 이동시킨다.
보면 알 수 있듯, grad_squared += dx*dx = 현 기울기의 제곱을 계산 후 더한 다음, 루트를 씌워 lr에 나눈다.
즉, 현재까지의 모든 기울기의 제곱을 더해, 루트 씌우고 lr에 나눈다.
이렇게 되면, 기울기가 충분히 크다면 lr이 작아져 조금씩 움직일테고, 기울기가 작다면 lr이 커져 크게 움직일 거다.
근데 문제는, 이 grad_squared가 누적되었다면? grad_squared는 누적되기 때문에 어쩔수 없이 커질 수밖에 없는 구조고, 언젠가는 극점에 다다를수록 학습률이 매우 저조해질 수밖에 없다.
만약 경사가 매우 가파른 곳에서 학습을 시작한다면, 초반부터 적응적 학습률이 급격히 감소하다가 최적해에 도착하기 전 조기 종료될 가능성이 있다. 이러한 조기중단 문제를 해결하기 위해 고안된 것이 RMSPROP이다.
4) RMSPROP:

이러한 H의 무한증가를 막기 위해, 각각에 가중치를 부여한다.
수정된 식을 보면 알 수 있지만, decay_rate(약 0.9)를 grad_squared에 부여함을 알 수 있다.
이 식을 통해, 여태 계속 누적된 h엔 0.9를, 현재 추가될 기울기엔 0.1을 곱함으로써,
과거의 기울기의 제곱들엔 큰 비중을, 현재 추가될 가중치엔 작은 비율을 준다.

꼴랑 0.1 곱하는게 무슨 비중이 큰 거냐고 생각할 수 있지만, 위의 수식을 보면 그렇지 않다는 것을 알 수 있다.
이전의 것들의 요소들은 계속해서 0.9의 제곱을 곱해나가기 때문에, 결국엔 매우 작은 비중을 차지하게 된다.
즉, 하나하나의 값들은 점차 미미해지지만 그 합한 것은 영향력을 발휘하는 것.
따라서, 이를 통해 최종적으로 미분값이 큰 곳에서는 업데이트 시 큰 값으로 나눠 작게 업데이트 시키고,
미분값이 작은 곳에서는 작은 값으로 나눠 기존 학습률보다 크게 업데이트 시키는 기조의 유지가 가능하다.
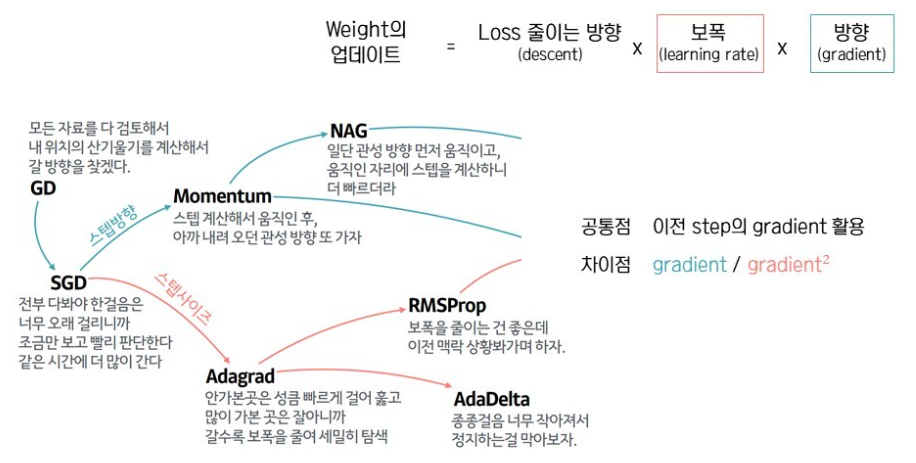
5) ADAM: 위의 2가지 부류인 Momentum과 Adagrad를 합친 것.
즉, 일부 자료만을 검토하는 SGD에서 분화된, local minima를 극복하기 위해 관성을 부여한 Momentum부류와, Step size를 조절하기 위해 Learning rate를 제곱합 축적등을 이용하는 Adagrad부류를 합하여, 보폭과 방향을 동시에 조절하는 방법이 설계.

beta1 = 0.9라 하자. momentum 과정에서, 과거의 기울기(혹은 그 합)에 0.9만큼, 현재 기울기엔 0.1만큼의 비중을 first moment에 저장한다.
먼저 Second_moment를 0으로 초기화한 상태. 업데이트를 한 번 진행하고 나면, second_moment의 decay rate인 'beta2'는 0.9 또는 0.99와 같이 1에 매우 가깝게 되고, 또 한 번의 업데이트 후에도 second_moment는 여전히 0에 가깝다.
여기에서 learning rate를 second_moment로 나누면 아주 작은 수로 나누게 되는 것으로, lr은 상당히 그 값이 커져 잘못된 방향으로 학습하게 될 수 있다.

따라서 bias를 넣음으로써 값이 확 튀지 않게 한다.

수식으로 옮겨넣으면 위와 같은 형태가 된다.
첫째로, Mt의 식에서 빨간색 박스 속 gt를 보니 이것은 gradient를 중심으로 하는 모멘텀 계열이라는 것을 알 수 있어요.
둘째로, 그 아래 파란색 박스 속 gt^2를 보니 vt는 gradient 제곱에 반비례하는 ada, rmsprop 계열이라는 것을 알 수 있죠.
마지막으로 mt와 vt모두 rmsprop 슬라이드에서 봤던 decay rate가 포함된 가중평균식과 비슷하다는 것을 알 수 있습니다.
Moment란 ‘적률’이라는 개념입니다. 기본적으로 통계학에서 n차 적률이라고 하면 Xn의 기댓값을 의미한다고 해요. 우리가 알고 있는 모평균은 원래 X의 1차 적률이었고, 분산을 구할 때 자주 등장하는 E(X^2) 이것은 X의 2차 적률이라고 불립니다. 우리는 표본평균과 표본제곱평균을 통해 모수에 해당하는 이 1차 적률과 2차 적률을 추정하는 거예요. 즉, Gradient의 1차 2차 moment에 대한 추정치는, 각각의 모수인 E(Gradient)와 E(Gradient2)를 추정하는 값을 가리키는 말입니다.

mt의 초기값(즉, m_(t-1))이 0이라면, 그와 곱해지는 β1은 1에 가까운 값(0.9)로 지정되어있기에, 기울기인 gt에 관계없이 (1−β1)gt는 0에 가까운 값이 되고, 결국 mt는 0에 가까워진다.
만일 이 mt가 그대로 가중치 업데이트 식에 쓰인다면, momentum의 상황을 고려하면, lr에 곱해질 경우, step 이동이 거의 없는, 즉 업데이트가 거의 되지 않는 결과를 보이게 된다. 따라서 이를 막기 위해, mt^ 식을 새로 만들어 적용한다.
다음으로 파란색을 보자. v의 초깃값 v_(t-1))이 0이라면, 그와 곱해지는 β2는 1에 가까운 값(0.999)로 지정되어 있기에, 기울기의 제곱인 gt^2의 값에 관계없이 (1−β2)gt^2는 0에 가까운 값이 되고, 결국 vt가 0에 가까워지게 된다.
이 vt가 그대로 아래 가중치 업데이트 식에 쓰이면, 기울기 제곱에 반비례하는 ada 계열의 특성인 vt1 부분의 값이 발산하게 되어, 한 step에 너무 많이 이동해버리는 편향된 결과를 보일 수 있다. 따라서 이러한 편향을 잡아주기 위해 vt대신 불편추정치를 계산하여 가중치 업데이트 식에 적용한다.
Optimizer 처음 링크에선 위와 같이 설명한다.
불편추정량에 대해서는
https://blog.naver.com/ao9364/222023124818
표본분산은 왜 n-1로 나눌까? : 자유도와 불편추정량 (feat. 표본평균의 평균과 분산 증명하기)
참고 이 포스트는 군소리는 최대한 배제하고 중요한 내용만 알차게 담기 위해 노력했으니 대충 앞부분만 읽...
blog.naver.com

결론이 뭐냐면, momentum의 문제점인 "가속도로 인한 기울기 진행 벡터의 급증가"와, Adagrad의 문제점인 "lr에 곱해지는 스칼라가 작아짐으로 인한 학습 step 감소"를 잘 버무려서 둘 사이의 약점을 상쇄한단 얘기.
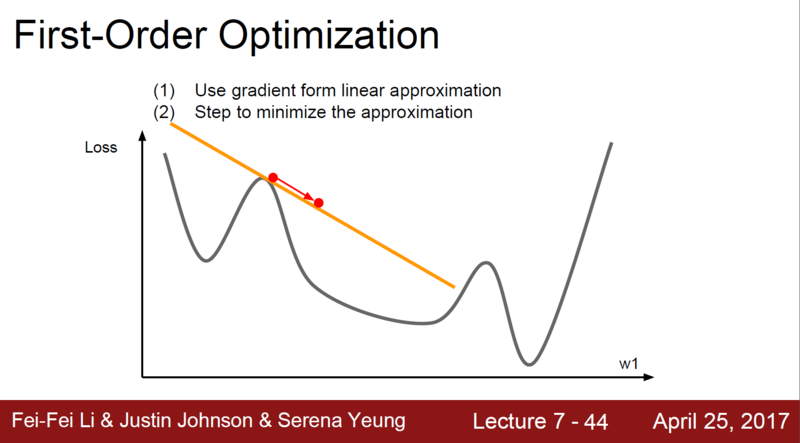
Gradient는 linear approximation하다. 그림을 보면 알 수 있듯, 해당 좌표 이후에 무슨 일이 일어날지 모르기 때문에, 곡선의 곡률을 고려하지 못한 채 error를 줄이는 과정을 거치게 된다.
이를 개선하고자 한 것이 Second-order approximation으로, gradient를 한번더 미분한 Hessian(헤시안)으로 에러를 줄일 방향과 크기를 결정하는 것이다.
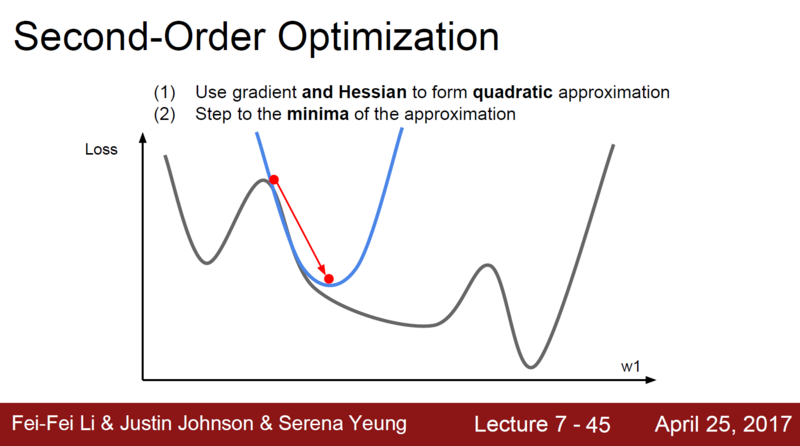
Hessian을 적용하면 에러가 더 잘 줄어드는 것을 확인할 수 있다.

헤시안을 사용하면 learning rate를 지정하지 않아도 된다는 장점이 있지만, 헤시안을 계산할때 Computational Complexity가 N의 제곱이고 여기다 Inverse를 취하면 N의 세제곱이기 때문에 딥러닝에서 사용하기 어렵다.

그래서 헤시안을 근사적으로 만드는 방법이 있는데, BGFS(Quasi-Newton method)와 L-BFGS(Limited memory BFGS)다.
선형대수학/역행렬이 왜 필요한가?
XW=Y 이런 식이 나왔었는데, 만약 여기서 W(가중치벡터)를 구하고 싶다!하면 지금 상태로는 할 수 없음
X(인풋데이터)가 남아있기 때문이다
따라서, 역행렬을 구하는 공식을 알아야 함. 그리고 주어진 행렬의 역행렬이 존재하는지를 결정하는 데 쓰는 게 행렬식.
'버츄얼유튜버' 카테고리의 다른 글
| 여러 CNN 아키텍처(LeNet, GoogleNet, Alexnet, VGG, ResNet) (0) | 2022.07.28 |
|---|---|
| Regularization (0) | 2022.07.27 |
| 통계 잡다 (0) | 2022.07.20 |
| 이미지분류 위한 공부 (0) | 2022.04.08 |
| 카스미자와미유가 쓰레기통에서 줏은 머신러닝 관련 글 (0) | 2022.04.02 |

