[CS231n 정리] 10. Recurrent Neural Networks (velog.io)
[CS231n 정리] 10. Recurrent Neural Networks
이 글은 단지 CS231n를 공부하고 정리하기 위한 글입니다.
velog.io
cs231n 10강 정리 - Recurrent Neural Networks (velog.io)
cs231n 10강 정리 - Recurrent Neural Networks
CS231n 10강강의 슬라이드one to oneone to manymany to onemany to manymany to manyMachine Learning 관점에서 생각해보면 모델이 다양한 입력을 처리할 수 있도록 유연해질 필요가 있습니다. 그런 관점에서 RNN은
velog.io

RNN에서는, 여러 종류의 input과 output에 대한 처리가 가능하다. 예를 들면
- one to one : 가장 기본적인 형태로 하나의 입력과 하나의 출력을 가지는 형태
- one to many : 하나의 입력에 대해서 여러 출력
- 예시 : image captioning - 하나의 사진에 대해 여러 단어를 출력
- many to one : 여러 입력에 대해서 하나의 출력
- 예시 : 감정구별
- many to many : 여러 입력에 대해서 여러 출력
- 입력에 대해 바로 출력이 나오는 경우 예시 : 비디오에 대해 프레임 단위로 classification
- 입력에 대해 시간차이가 존재하는 경우 예시 : 기계번역

RNN의 수식

xt : 입력
ht-1 : 전 hidden state
fW : 현재 hidden state를 구하는 함수
ht : 현재 hidden state
모든 함수와 parameter값을 모든 시간에서 동일하게 사용하는 것이 MLP와의 차이점이라 볼 수 있다.
좌측의 수식을 살펴본다.
ht는, 이전 ht-1과 인풋값 xt를 받으면,
이를 fw처리해 그 상태에서의 hidden state를 구한, 즉 아웃풋이다.

1) 가중치 행렬 와 입력
가중치 행렬 이전 hidden state 값인 와 곱한다.
3) 두 입력 에 대한 행렬 곱 연산의 결과 값을 더한다.
4) non-linearity를 위해 를 사용한다.
위 그림을 보면 알 수 있듯, x(=학습 데이터셋)이 n개의 벡터(단어)로 구성된 하나의 set이며, 이것들이 다음 Hidden layer들과 fully connected된 상태이다.
또한 가중치행렬이 무려 3개인데, 각각 x에서 RNN을 하는 과정에서 처리하는 것, h=현재 hidden state를 갱신하는 가중치, RNN처리 후 결과값 내는 데 쓰이는 가중치가 있다.


이를 도식화하면 옆과 같다.
동일한 가중치행렬 W를 매번 사용한다.
이로 인해, 이 RNN모델의 역전파를 위한 Gradient를 구하기 위해선, 각 step에[서의 W에 대한 gradient를 전부 계산한 다음, 이를 모두 더하면 된다.
그리고 L은 손실이다.
각 시퀀스마다 Ground Truth Label이 있다면, 각 스텝마다 개별적으로 yt에 대한 Loss(=소프트맥스 loss)의 계산이 가능하다. 이 개별 loss들의 합이 RNN의 최종 Loss다.
모델을 학습 시키기 위해 를 구해야 한다. 이 Loss flowing은 각 time stpe마다 가중치 에 대한 local gradient를 계산하고, 이 local gradient을 최종 gradient에 더함으로써 구할 수 있다.
이부분은 맨 위 링크의 복붙.
one to many
그렇다면 one to many의 경우는 어떨까요?

fix sized input을 받지만, variably sized output인 network입니다.
이 경우에는 대부분 고정 입력은 모델의 initial hidden state을 초기화 시키는 용도로 사용하고, RNN은 모든 step에서 output을 가집니다.
고정 입력을 받지만 가변 출력인 네트워크입니다. 이 경우에는 대체적으로 고정 입력은 모델의 initial hidden state를 초기화 시키는 용도로 사용합니다.
그리고 RNN은 모든 스텝에서 출력 값을 가집니다.
이렇게 가변 출력을 가지는 경우에도 그래프를 Unroll 할 수 있습니다.
Sequence to Sequence: Many-to-one + one-to-many

machine translation에 쓰이는 Sequence to Sequence 모델에 대해서 알아보겠습니다.
이것은 두 개의 스테이지로 구성됩니다.
- encoder
- decoder
구조입니다.
encoder은 가변 입력을 받습니다. 예를 들면, English sentence가 될 수 있습니다.
encoder의 final hidden state를 통해 전체 sentence를 요약합니다.
encoder에서는 many to one을 수행합니다. 가변 입력을 하나의 vector로 요약합니다.
decoder은 one to many를 수행합니다. 입력은 앞서 요약한 하나의 vector가 되었는데요. decoder는 가변 출력을 내뱉습니다.
예를 들여, 아까 입력 받은 문장을 다른 언어로 번역된 문장이 될 수 있습니다.
가변 출력은 매 step마다 적절한 단어를 출력합니다.
그럼 전체 Computational graph를 풀어서 전체 학습 과정을 해석해보면 Output sentence의 각 loss들을 합해 Backprob을 진행합니다.
RNN 예시

네트워크가 문자열 시퀀스를 읽어왔고, 현재 문맥에서 helllo를 에측해야 한다하자. 리스트로는 [h, e. l, o]로 표현된다.
Train time에서는 training sequence(hello)의 각 단어를 입력으로 넣어줘야 한다.
- 'hello'가 RNN의
- vocab은 4개.
각 글자는 하나의 vector로 표현이 가능하며, 이 vector는 1이 하나 있고 나머지는 0인 vector. vector에서 해당 글자의 위치에서만 1로 표시를 해주는 것.
- [1,0,0,0]
- [0,1,0,0]
- [0,0,1,0]
- [0,0,0,1]
각각이 h, e, l, o를 표현한 것. 위의 사진에서 확인이 가능하다.
이 네트워크의 목적은, hell을 입력받을 때 다음에 올 o를 출력하여, hello를 추측하는 모델이다.
먼저 위처럼 각 단어를 원핫인코딩으로 변환해 입력으로 넣는다.

Forward pass에서 네트워크의 동작은 첫 번째 step에서는 입력 문자 h가 들어오고, 첫 번째 RNN cell로는 'h'가 들어간다.
[구조도] 그림을 보면 알 수 있듯, 출력값 어떤 문자가 'h' 다음에 나올 것 같은 지를 예측한 값.
이 과정을 반복하며 모델을 다양한 문장으로 학습시켜, 이전 문장의 문맥을 참고하여 다음 문자가 무엇인지를 학습.

각 입력에 대한 출력을 Sampling해서 다음 입력으로 넣는 경우도 있다고 한다.
- Softmax를 추가하여 다른 값보다 얼마나 높은지를 추정하고, 다른 값들과 상호 배타적(mutually exclusive)으로 비교
- 이로써 Cross Entropy 오차로 사용
- 아래를 보면 알 수 있듯, 가장 값이 큰 건 4.1이지만, 사용하는건 2.2다. 즉 max를 쓰지 않는다. 학습이 잘 안되기에. 출력은 o가 되었지만, 학습시 다음 입력은 target인 e를 넣어서 학습시키는 것.

확률 분포에서 'e'가 나왔고, 이를 다음 스텝의 네트워크 입력으로 넣어준다. 'e'를 다시 vector [0,1,0,0]으로 만들어주고 그 다음 input으로 넣어주면 네트워크는 두 번째 출력을 만들어낸다.

이렇게 학습된 모델만 가지고 새로운 문장을 만들어 내기 위해, time step마다 확률분포에서 문자를 하나씩 뽑아내며 문장을 완성한다.
backpropagation through time

손실값에 대해선, 위의 [구조도]에 상세히 설명되어 있다.
forward pass의 경우, 전체 sequence가 끝날 때까지 출력값이 생김을 위에서 보였다.
반대로 backward pass에서도 전체 sequence를 갖고 Loss를 계산해야 한다.
그런데, 이 sequence가 아주 길다면. gradient를 계산하는데 매우 시간이 오래 걸린다.
만약 위키디피아에 있는 모든 문서를 바탕으로 학습을 한다면 전체 문서를 다 거쳐야 한다!
이 전체 문서에 대한 gradient를 계산하고 나면 gradient 업데이트가 겨우 1회 수행된 꼴로, 이를 반복해서 학습시키는 과정은 아주 느릴 것이고, 메모리 부족의 문제로도 이어질 것이다.
만일 many-to-many를 학습하는 과정에서 발생하는 Loss에 대해 각각의 가중치를 업데이트하려면, 위와 같이 한번에 전체적으로 gradient를 계산하여 backpropagation을 진행해야 할 것이다. sequence가 매우 긴 경우에는 계산하는데 엄청난 시간을 필요로 할 것이다. 정말 느린학습이 예상된다.
Truncated Backpropagaiton

그래서 Truncated Backpropagaiton이라는 방법을 통해 backprop을 근사시키는 기법을 사용한다.
이는, input sequence가 매우 길다면, 이를 train time에 하나의 step을 일정 단위로 자른다는 것이다.
만약 100정도로 자른다고 하면, 100 step만 forward pass하고 이 sub sequence의 loss를 계산, gradient step을 진행한다.
이전 batch(=100)에서 계산한 hidden states를 계속 유지하면서 이를 반복한다.
다음 Batch의 forward pass를 계산할 때는 이전 hidden state를 이용한다. gradient step은 현재 Batch에서만 진행한다.
즉, 일부만 잘라서 얘네들끼리 loss 구하고 얘네들끼리 가중치 변경하는 걸 진행. Loss판 mini-batch라 생각.
1) 순환 신경망(Recurrent Neural Network, RNN) - 딥 러닝을 이용한 자연어 처리 입문 (wikidocs.net)
1) 순환 신경망(Recurrent Neural Network, RNN)
RNN(Recurrent Neural Network)은 입력과 출력을 시퀀스 단위로 처리하는 시퀀스(Sequence) 모델입니다. 번역기를 생각해보면 입력은 번역하고자 하는 ...
wikidocs.net
RNN은 은닉층의 노드에서 활성화 함수를 통해 나온 결과값을 출력층 방향으로도 보내면서, 다시 은닉층 노드의 다음 계산의 입력으로 보내는 특징을 갖고있다.

위의 그림을 보겠습니다. x는 입력층의 입력 벡터, y는 출력층의 출력 벡터입니다.
RNN에서 은닉층에서 활성화 함수를 통해 결과를 내보내는 역할을 하는 노드를 셀(cell)이라고 합니다. 이 셀은 이전의 값을 기억하려고 하는 일종의 메모리 역할을 수행하므로 이를 메모리 셀 또는 RNN 셀이라고 표현합니다.

은닉층의 메모리 셀은 각각의 시점(time step)에서 바로 이전 시점에서의 은닉층의 메모리 셀에서 나온 값을 자신의 입력으로 사용하는 재귀적 활동을 하고 있습니다. 앞으로는 현재 시점을 변수 t로 표현하겠습니다. 이는 현재 시점 t에서의 메모리 셀이 갖고있는 값은 과거의 메모리 셀들의 값에 영향을 받은 것임을 의미합니다.
그렇다면 메모리 셀이 갖고 있는 이 값은 뭐라고 부를까요?
메모리 셀이 출력층 방향 또는 다음 시점인 t+1의 자신에게 보내는 값을 은닉 상태(hidden state) 라고 합니다. 다시 말해 t 시점의 메모리 셀은 t-1 시점의 메모리 셀이 보낸 은닉 상태값을 t 시점의 은닉 상태 계산을 위한 입력값으로 사용합니다.
RNN Language model - latent structure
RNN Language model로 어떤 문장이든 학습 시킬 수 있다. 아래는 세익스피어의 소설을 예로 든다.
학습 초기에는 의미없는 문장만 내지만, 학습을 시킬 수록 의미 있는 문장을 만들어낸다.
학습이 끝나면 셰익스피어 느낌을 내는 문장을 만들어 낼 수 있다.

여기서 알아야 할 점은 우리가 모델에게 요청한 것이 Sequence의 다음 문자를 예측하는 것이라는 것이다.
모델은 학습 과정 속에서 시퀀스 데이터의 숨겨진 구조(latent structure)을 알아서 학습한다.
모델이 어떤 방식으로 학습하는가?
Searching for interpretable cells
RNN에는 hidden vector가 있고 이 vector가 계속 업데이트 된다.
그 vector를 추출해보면, 해석 가능한 의미 있는 것들이 올 수도 있지 않을까하는 추측에서 출발해보자.

서로 다른 hidden states가 도대체 어떤 것을 중요시하게 보고 있는지 알아보기 위해,
RNN Language model을 특정 dataset으로만 학습시키고, hidden vector을 하나 뽑아서 어떤 값이 들어있는지 살펴보았다.

vector를 하나 뽑은 다음에 이 시퀀스를 한 번 forward 시켜보았다.
여기서 각 색깔은 시퀀스를 읽는 동안에 앞서 뽑은 hidden vector의 값을 의미한다.

대부분의 cell은 의미를 파악하기 어렵지만, 따옴표(quote)를 찾는 벡터를 알아냈다. 잘 보면 따옴표가 시작하는 부분 " " 이 각각 다른 색깔의 블록으로 표시되어 있음을 알 수 있다.

또한, 이곳에서는 줄바꿈을 위해 현재 줄의 단어 갯수를 세는 듯해 보이는 Cell도 발견했다.
처음에는 0으로 시작했다가 줄이 점점 길어지면 점점 빨간색으로 변하는데, 점점 길어지다 줄바꿈이 이루어지면 다시 0으로 리셋된다. 이 cell은 언제 모델이 new line characters을 필요로 할 지 지속적으로 추적하는 역할을 수행한다.
그저 다음 문자를 예측해달라는 모델을 학습했을 뿐인데 모델은 입력 데이터의 구조를 학습하게 되었다.
Image Caption

RNN을 이미지에 적용시켜보자.
Image Captioning은 이미지의 정보를 CNN을 통해 summary vector로 학습하고, RNN을 통해 그에 해당하는 문장을 만들어 내는 모델이다. 학습이 진행될때는 RNN에서 CNN으로 gradient를 넘겨준다.

모델에는 입력 이미지를 받기 위한 CNN이 있으며, 이는 요약된 이미지 정보가 들어 있는 Vector를 출력한다.
이 Vector는 RNN의 초기 step의 입력으로 들어가며, 이 때 RNN은 caption에 사용할 문자를 하나씩 만들어낸다.

전체 구조를 살펴보자.
- 입력 이미지를 받아 CNN의 입력으로 넣는다. 이 vector는 전체 이미지 정보를 요약하는데 사용될 것이다.
- 다만 sofemax scores를 사용하지 않고 직전의 4,096-dim vector를 출력한다.

- RNN Language models에서 배웠듯이, 모델이 문장을 생성해 내기 위해 앞서 초기 값을 넣어준다.
이제는, 이미지를 주고 문장을 만들어달라는 요구로 시작할 것이다.

이전까지의 모델에서는 RNN 모델이 현재 스텝의 입력, 이전 스텝의 Hidden state라는 두 개의 가중치 행렬을 입력으로 받아 조합하여 다음 Hidden state를 획득했다. 그러나 이젠 이미지 정보도 추가를 해줘야 하기에, Wih * v라는 세 번째 가중치 행렬을 추가했다. 이를 통해, 다음 hidden state를 계산할 때마다 모든 스텝에서 이미지 정보를 추가할 수 있게 된다.

- Vocabulary의 모든 scores에 대한 분포를 계산

이 문제에서 Vocabulary는 위키디피아의 전체 문서보다 더 크다고 생각하면 된다.
그 분포에서 sampling을 하고 그 단어를 다음 스텝의 입력으로 다시 넣어준다. sampling 된 가 들어가면 다시 vocab에 대한 분포를 추정하고 다음 단어를 만들어 낸다. 이러한 모든 스텝이 종료되면 한 문장이 만들어진다.

이때 <'END'>라는 특별한 토큰이 있는데 이는 문장의 끝을 알려주는 토큰이다. 이 토큰이 sampling되면 모델은 더 단어를 생성하지 않고 이미지에 대한 caption을 완성한다.
Train time에는 네트워크가 학습하는 동안 시퀀스의 끝에 토큰을 넣어야 한다는 것을 알려줘야 하기 때문에 모든 caption의 종료 지점에 토큰을 삽입한다. 이렇게 학습이 끝나게 되면, Test time에는 모델이 문장 생성을 끝마치고 토큰을 샘플링한다.
이 Task를 위한 가장 큰 데이터 셋은 Microsoft COCO 데이터셋이 있는데, 이 모델을 학습시키기 위해서 natural language model과 CNN을 동시에 backprop 할 수 있다.


모델을 학습한 후 나온 결과.
잘못 예측한 경우는 Train time에서 잘 발견하지 못한 데이터인 경우인데, 모델은 Train time에서 본 사실만 배우기 때문이다. 그럼에도 꽤나 잘 맞춘 모습.
Image Captioning with Attention

조금 더 발전된 Attention이란 모델이 있다. cs231n에서는 상세히 다루지는 않는다.

CNN으로 벡터 하나를 만드는 것이 아닌 공간 정보를 가지고 있는 grid of vector를 만들어낸다.
Forward pass시 매 스텝 voca에서 샘플링 할 때, 모델이 이미지에서 보고 싶은 위치에 대한 분포를 만들어낸다.
이미지의 각 위치에 대한 분포는 Train time에 모델이 어느 위치를 봐야하는 지에 대한 'Attention'이라 할 수 있다.

Train을 끝마치면 모델이 caption을 생성하기 위해 이미지의 attention을 이동시키는 모습을 볼 수 있다.
이 caption을 만들어 내기 위해 이미지 내에 다양한 곳들에 attention을 주는 것을 확인할 수 있다.

위의 예시를 보아도, 여자가 원반을 던진다 라는 caption을 만들어 냈고, 이미지에서 원반에 attention하고 있다.
모델에서 매 스텝마다 어디를 보라고 말해준 적이 없는데도 잘 생성한다.
모델 스스로가 Train time에서 알아냈다. 모델이 원반 영역에 집중하는 것이 가장 올바른 일이라는 걸 스스로 알아낸 것.
모델 전체가 미분이 가능하기 때문에 soft attention 또한 backprop이 가능.
RNN + Attention
이 조합은 Image captioning 뿐만 아니라 더 다양한 것들을 할 수 있다.

Visual Question Answering이 있다. 여기서는 입력이 두 개로, 하나는 이미지와 하나는 이미지에 관련된 질문
이 모델 또한 RNN과 CNN으로 만들 수 있다.

이 경우는 "many to one"의 경우. 모델은 자연어 문장(질문)을 입력으로 받아야 한다. RNN으로 구현할 수 있고, RNN이 질문을 vector로 요약. 그리고 여기서는 이미지 요약이 필요하기 때문에 CNN이 필요한다.
RNN/CNN에서 나온 벡터를 조합하면 질문에 대한 분포를 예측할 수 있다.
이 부분은 빠르게 pass.
Multilayer RNNs
지금까지는 RNN 레이어를 단일로 사용했으며, 따라서 hidden state가 하나 뿐이었다. 하지만 더 자주 보게 될 모델들은 Multilayer RNN로,

위 이미지에는 3-Layer RNN이 있다. 입력이 첫 번째 RNN으로 들어가서 첫 번째 hidden state를 만들어낸다.
RNN 하나를 돌리면 hidden state 시퀀스가 생기며, 이를 다른 RNN의 입력으로 넣어줄 수 있다.
그러면 두 번째 RNN layer가 만들어내는 또 다른 hidden states 시퀀스가 생겨난다. 이런 식으로 RNN layer를 쌓아 올릴 수 있으며, 이를 통해, 모델이 깊어질수록 다양한 문제들에서의 성능 향상을 꾀할 수 있다. 보통은 일반적으로 2~4 layer RNN이 적절하다고 한다.
Vanilla RNN Gradient Flow

RNN 사용할 때 문제점이 있는데, 현재 입력 x_t, h_t-1(이전 hidden state)가 있고 이 두 입력을 쌓는다(stack). 이렇게 두 입력을 쌓고 가중치 행렬 W와 행렬 곱 연산을 하고 tanh를 씌어 다음 hidden state(h_t)를 만든다.
이게 일반적인 RNN의 수행인데, 그러면 이 아키텍처는 backward pass에 그레디언트를 계산하는 과정에서 어떤 일이 발생할까?

일단 Backward pass시 h_t에 대한 loss의 미분값을 얻는다. 그 다음 Loss에 대한 h_t-1의 미분값을 계산하게 된다. Backward pass의 전체 과정은 빨간색 통로를 따라가면 됩니다.
우선 그레디언트가 tanh gate를 타고 흘러가고, Mat mul gate를 통과한다. Mat mul gate의 back prop은 결국 이 transpose(가중치 행렬)을 곱하게 된다.
이는 매번 vanilla RNN cells를 하나 통과할 때마다 가중치 행렬의 일부를 곱하게 된다는 의미인데, RNN의 특성 상, RNN이 여러 시퀀스의 Cell을 쌓아 올리는 사실을 고려하면 그레디언트가 RNN 모델의 Layers 시퀀스를 통해 어떤 방식으로 전달되는지 생각해 볼 수 있다.

그런데 만약 우리가 h_0에 대한 그레디언트를 구하고자 한다면 결국 모든 RNN Cells를 거쳐야 한다는 것을 알 수 있다.
이는 cell이 하나를 통과할 때마다 각 cell의 행렬 W transpose factors가 관여하고, h_0의 그레디언트를 계산하는 식을 써보면 아주 많은 가중치 행렬이 개입하게 되는 것을 알 수 있다. 이는 매우 계산량이 많아지게 된다.
설령 가중치가 행렬이 아니라 스칼라라고 생각해도, 이 값들을 계속해서 곱한다고 했을 때, 값들을 수백 번 곱해야 할 수도 있다.
이로 인해 발생하는 문제점은 이전에 설명한 바 있다.
- 만약 스칼라가 엄청 크다면? h_0의 그레디언트는 아주 커지게 된다. 이를 Exploding gradients라고 한다. backprop시 레이어가 깊어질 수록 그레디언트가 기하급수적으로 증가하는 현상.
- 행렬의 특이값이 1보다 작은 경우라면 정반대의 상황이 발생합니다. 그레디언트가 기하급수적으로 작아진다. 이를 Vanising gradients라고 한다.

그래서 사람들은 gradient clipping 이라는 기법을 사용한다. 이는 즉, 그레디언트를 계산하고 그레디언트의 L2 norm이 임계값보다 큰 경우 그레디언트가 최대 임계값을 넘지 못하도록 조정하는 것이다.
하지만 반대로 Vanising gradients를 다루려면 더 복잡한 RNN 아케틱처가 필요하다. 이를 위해 개선된 것이 LSTM.
Long Short Term Memory (LSTM)
https://dgkim5360.tistory.com/entry/understanding-long-short-term-memory-lstm-kr
Long Short-Term Memory (LSTM) 이해하기
이 글은 Christopher Olah가 2015년 8월에 쓴 글을 우리 말로 번역한 것이다. Recurrent neural network의 개념을 쉽게 설명했고, 그 중 획기적인 모델인 LSTM을 이론적으로 이해할 수 있도록 좋은 그림과 함께
dgkim5360.tistory.com


"I grew up in France ... I speak fluent French" 라는 문장의 마지막 단어를 무엇인지 파악하고자 할 때, RNN구조에서는 최근 몇몇 단어를 볼 때 아마 언어에 대한 단어가 와야 되리라 추측은 가능하지만, 어느 나라 언어인지 알기 위해선, 프랑스에 대한 문맥을 훨씬 뒤에서 찾아야 한다. RNN구조의 문제점이 여기에 있다. 뒤에 있는 걸 찾기 위한 시간이 아주 오래걸린다. 즉, 짧은 건 몰라도, 긴 기간에 대한 의존성에 매우 취약하다.


LSTM의 핵심 아이디어
LSTM의 핵심은 cell state로, 모듈 그림에서 수평으로 그어진 윗선에 해당한다.
보면 알 수 있듯, 작은 linear interaction만을 적용시키면서 전체 체인을 계속 구동시킨다.
이 cell state의 목적은, 각 gate의 결과를 더하는 update를 통해, 시퀀스가 길더라도 gradient, 즉 오차를 상대적으로 잘 전파시키도록 위함이다.
Gate라 불리는 구조는 이 cell state에 뭔가를 더하거나 없앨 수 있는 제어능력을 지닌다.
Gate는 정보가 전달될 수 있는 추가적인 방법으로, sigmoid layer와 pointwise 곱셈으로 이루어져 있다.
Sigmoid layer는 0과 1 사이의 숫자를 내보내는데, 이 값은 각 컴포넌트가 얼마나 정보를 전달해야 하는지에 대한 척도를 나타낸다. 그 값이 0이라면 "아무 것도 넘기지 말라"가 되고, 값이 1이라면 "모든 것을 넘겨드려라"가 된다.
LSTM은 3개의 gate를 가지고 있고, 이 문들은 cell state를 보호하고 제어한다.
단계별로 두들겨보는 LSTM
1) 앞서 말했듯, Sigmoid Layer에서는, cell state로부터 어떤 정보를 버릴 것인지를 정한다. 그래서 이 단계의 gate를 "forget gate layer"라고 부른다. 이 단계에서는 x_t를 받아서, 0과 1 사이의 값을 에 보내준다. 그 값이 1이면 "모든 정보를 보존해라"가 되고, 0이면 "죄다 갖다버려라"가 된다.
아까 얘기했던 이전 단어들을 바탕으로 다음 단어를 예측하는 언어 모델 문제로 돌아가보겠다. 여기서 cell state는 현재 주어의 성별 정보를 가지고 있을 수도 있어서, 그 성별에 맞는 대명사가 사용되도록 준비하고 있을 수도 있을 것이다. 그런데 이 때 새로운 주어가 온다면, 이 새 주어의 대명사를 써야할 테니 기존 주어의 성별 정보는 갖고 있을 필요가 없게 된다.
2) 다음 단계는, 앞으로 들어오는 새로운 정보 중 어떤 것을 cell state에 저장할 것인지를 정한다. 먼저, "input gate layer"라고 불리는 sigmoid layer가 어떤 값을 업데이트할 지 정한다. 그 다음에 tanh layer가 새로운 후보 값들인 라는 vector를 만들고, cell state에 더할 준비를 한다. 이렇게 두 단계에서 나온 정보를 합쳐서 state를 업데이트할 재료를 만들게 된다.
언어모델 예제로 돌아오면, 1단계에서 기존 주어의 성별을 잊어버리기로 했고, 그 대신 새로운 주어의 성별 정보를 cell state에 더하고자 하는 것이다.
3) 과거 state인 를 업데이트해서 새로운 cell state인 를 만들 것이다. 이미 이전 단계에서 어떤 값을 얼마나 업데이트해야 할 지 다 정해놨으므로 여기서는 그 일을 실천만 하면 된다.
우선 이전 state에 를 곱해서 가장 첫 단계에서 잊어버리기로 정했던 것들을 진짜로 잊어버린다. 그리고나서 를 더한다. 이 더하는 값은 두 번째 단계에서 업데이트하기로 한 값(~Ct)을 얼마나 업데이트할 지 정한 만큼 scale(it)한 값이 된다.
또 다시 언어 모델 문제로 돌아가보면, 이 단계에서 실제로 이전 주어의 성별 정보를 없애고 새로운 정보를 더하게 되는데, 이는 지난 단계들에서 다 정했던 것들을 실천만 하는 단계임을 다시 확인할 수 있다.

4) 마지막으로 무엇을 output으로 내보낼 지 정하는 일이 남았다. 이 output은 cell state를 바탕으로 필터된 값이 될 것이다. 가장 먼저, sigmoid layer에 input 데이터를 태워서 cell state의 어느 부분을 output으로 내보낼 지를 정한다. 그리고나서 cell state를 tanh layer에 태워서 -1과 1 사이의 값을 받은 뒤에 방금 전에 계산한 sigmoid gate의 output과 곱한다. 그렇게 하면 우리가 output으로 보내고자 하는 부분만 내보낼 수 있게 된다.
이제 언어 모델 예제를 생각해보면, 우리는 주어를 input(xt)으로 받았으므로 주어 다음에 오게 될 예측값인 output(ht)으로 적절한 답은 아마도 동사 개념의 무언가가 될 것이다. 예를 들어 최종적인 Output은 앞에서 본 주어가 단수형인지 복수형인지에 따라 그 형태가 달라질 수도 있는 것이다.
LSTM의 변형 모델들
유명한 LSTM의 변형 모델 중 하나로 Gers & Schmidhuber (2000)가 소개한 것이 있는데, "엿보기 구멍(peephole connection)"을 추가한 모델이다. Gate layer들이 cell state를 쳐다보게 만드는 모델이기 때문에 이런 이름이 붙여졌다.
위 그림에서는 모든 gate마다 엿보기 구멍을 달아놨는데, 논문마다 엿보기 구멍을 어디엔 달고 어디엔 안 달고 할 수 있다. 혹은 Forget gate와 input gate가 합쳐져, 무엇을 잊어버릴지와 새로운 정보를 어느 부분에 더할 지를 따로 생각하지 않고, 한 번에 결정을 내리는 다른 변형 모델도 있다. 이 모델은 새로운 정보가 들어가는 자리만 잊어버린다. 그리고 이전 정보를 잊어버리는 부분만 새로운 값을 넣게 된다. 그 이미지는 아래와 같다.
LSTM이 조금 더 변형된 것으로 Gated Recurrent Unit (이하 GRU)가 Cho 외 (2014)에서 소개되었다. 이 모델은 forget gate와 input gate를 하나의 "update gate" 합쳤고, cell state와 hidden state를 합쳤고, 또 다른 여러 변경점이 있다. 결과적으로 GRU는 기존 LSTM보다 단순한 구조를 가진다. GRU는 점점 더 유명해지고 있다.
지금까지 소개한 LSTM의 변형 모델들은 극히 일부분일 뿐이다. 하나만 더 언급하자면 Yao 외 (2015)에서 소개한 Depth Gated RNN도 있다. 또한 Koutnik 외 (2015)처럼, LSTM와 다른 방식으로 긴 의존 기간을 해결하는 모델도 있다.
어떤 변형 모델이 가장 좋을까? 각 모델들의 다른 점들이 얼마나 중요하게 작용할까? Greff 외 (2015)에서 유명한 변형 모델들을 잘 비교했는데, 그 결과가 거의 비슷하게 나왔다. Jozefowicz 외 (2015)에서는 만 개가 넘는 RNN 모델을 시험해봤고, 어떤 문제냐에 따라 LSTM보다 좋은 결과를 내는 모델도 있음을 시사했다.
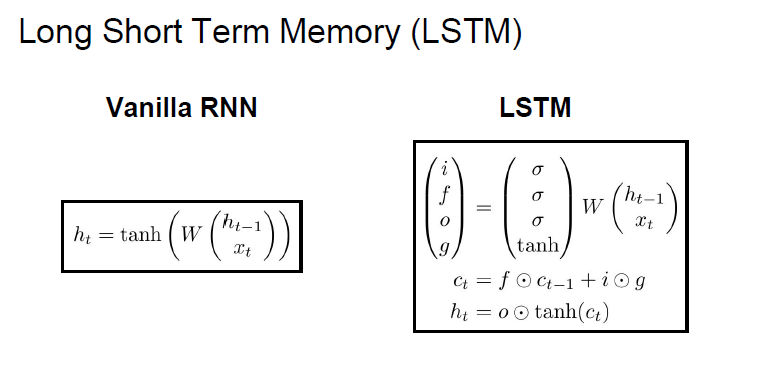
LSTM은 Exploding gradients, Vanising gradients 문제를 완화시키기 위해 디자인 되었다.
hidden state가 이었던 vanillia RNN은 매 스텝마다 재귀적 방법으로 hidden state를 업데이트 했다.
LSTM에는 한 cell 당 두 개의 Hidden state가 있다. 하나는 h_t이고, 하나는 c_t라는 두 번째 벡터이다. 이는 'Cell state'라고도 불린다.
Cell state는 LSTM 내부에만 존재하며 밖에 노출되지 않는 변수이며, h_t는 실제로 밖으로 보여지는 값이다.
LSTM은 (h_t-1, x_t) 2개의 입력을 받으며, [i, f, o, g]의 4개의 게이트를 계산한다.
이 게이트들은 cell_states, c_t를 업데이트하는데 쓰이며, 이 c_t는 다음 스텝의 hidden state를 업데이트하는 데 쓰인다.
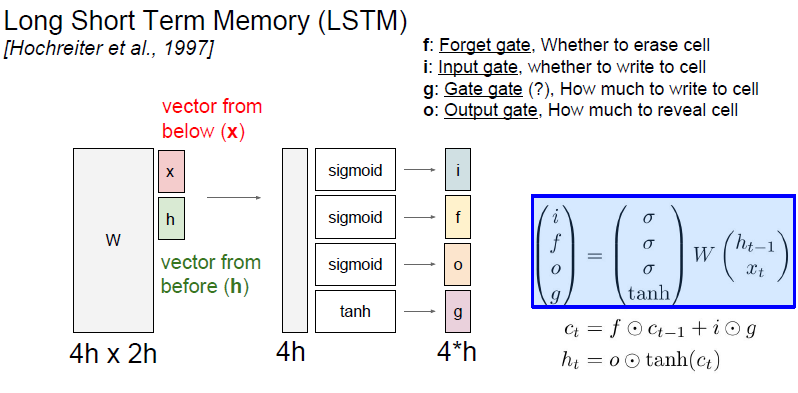
LSTM에서는 이전 hidden state인 h_t와 현재의 입력인 x_t를 입력으로 받는다.
단, 두 입력을 concat하고 행렬 곱 연산으로 hidden state를 직접 구하는 vanillia RNN과 약간 다르다.
LSTM은 이전 hidden state를 입력 받아 쌓아두고, 네 개의 gates의 값을 계산하기 위해 커다란 가중치 행렬을 곱해준다.
- input gate (시그모이드) : 이하 시그모이드 모두 [0, 1]의 값을 갖는다. cell state의 각 element에 대해 이 cell state를 사용하고 싶을 때 1이 되고, 그렇지 않을 때 0이 된다.
- forget gate (시그모이드) : 0일 떄, element는 이전 cell state를 잊고, 1일 때는 기억한다. 이전 cell state의 on/off를 기억.
- output gate (시그모이드) :
- gate gate (tanh) : input cell을 얼마나 포함시킬지 결정하는 가중치, [-1, 1]의 값을 갖는다.
이전 스텝의 Cell state(C_t-1)은 forget gate와 element-wise multiplication하다. 결과 벡터(f*c_t-1)는 0 또는 1 일 것.
cell state를 계산하는 전체 수식은 아래와 같다. 이 수식은 두 개의 독립적인 scaler 값 (f,i)에 의해 조정된다.

c_t의 수식은 이전 cell state(c_t-1)을 계속 기억할 지 말지를 결정한다. (f*c_t-1)
즉, cell state의 각 요소는 scalar integer counters처럼, 값이 줄었다 한다고 한다.
Cell state를 계산한 후에는 hidden state를 업데이트 할 차례이다. 각 스텝마다 최대 1 또는 -1씩 세고, 이 값은 tanh를 통과하여 최종적으로 output gate와 곱해집니다.
output gate 역시 sigmoid에서 나온 값이기 때문에 0~1 값을 가지며, output gate는 hidden gate를 계산할 때 cell state를 얼마나 노출시킬지를 결정한다.
LSTM Gradient Flow

왼쪽을 보면 이전의 의 입력값이 있네요. 현재 입력 도 있습니다. 우선 이 현재 입력 를 쌓습니다. 그리고 여기서 가중치 행렬 4개를 곱해 gate를 만드네요.
그리고 f는 이전 와 곱합니다. 그리고 i, g가 element wise로 곱한 후 cell state와 곱해 다음 을 만듭니다.
는 를 거친 후 o와 곱해져서 다음 hidden state()를 만들어냅니다.
각 gate는 각 gate마다 곱해지는 가중치 행렬을 갖고 있습니다. 우선 x와 h를 쌓으면 전체 행렬이 됩니다. 그리고 가중치 행렬의 크기는 입니다. 이 가중치 행렬은 행렬 4개를 서로 합쳐 놓은 것이라 보면 됩니다. 각 4개의 행렬은 서로 가능 gate를 계산합니다.
하지만 결국은 모두 두 개의 입력를 쌓고 행렬 곱 연산을 수행하는 것입니다!
이제 LSTM의 Backward pass를 보겠습니다. 앞서 vanilla RNN의 경우 Backward pass의 문제점이 무엇이었습니까?
- 가중치 행렬 w가 계속해서 곱해지는 문제
하지만 LSTM에서는 상황이 많이 달라집니다.

cell state에서 내려오는 upstream gradient를 살펴 봅니다. 우선 addition operation의 Backprob이 있습니다.
그레디언트는 upstream gradient와 forget gate의 element wise입니다. 그래서 upstream gradient * forget gate가 됩니다.
이게 vanilla RNN 보다 좋은 점이 2가지 있습니다.
- f와 곱해지는 연산이 matrix multiplication이 아닌 element-wise라는 점입니다.
full matrix multiplication 보다 element wise multiplication이 더 낫습니다. - element wise multiplication을 통해 매 스텝 다른 값의 f와 곱해질 수 있다는 점입니다.
앞서 vanilla RNN의 경우에는 동일한 가중치 행렬(h_t)만을 계속 곱했습니다. 이는 exploding/vanishing gradient 문제를 일으켰었는데, 반면 LSTM에서는 f가 스텝마다 계속 변합니다!
따라서 LSTM은 exploding/vanishing gradient 문제를 더 쉽게 해결합니다.
그리고 f는 sigmoid에서 나온 값이므로 element wise multply가 0~1 사이의 값입니다.
f를 반복적으로 곱한다고 했을 때 더 좋은 수치적인 특성으로 변합니다.
또 한 가지 명심해야 할 점!
vanilla RNN의 backward pass에서는 매 스텝에서 그레디언트가 어디를 거쳤죠? tanh를 거쳤습니다. LSTM에서도 hidden state h_t를 출력 y_t를 계산하는데 사용합니다.
만약 LSTM의 최종 hidden state h_t를 가장 첫 cell state(c_0)까지 backprop하는 걸 생각해보면, RNN처럼 매 스텝마다 tanh를 거칠 필요가 앖으며 단 한 번만 tanh를 거치면 됩니다.

LSTM의 전체적인 모습을 그려보니 cell state를 통한 backprop은 그레디언트를 위한 고속도로처럼 보입니다.
그레디언트가 모델의 종단인 Loss에서 가장 처음 cell state(C_0)까지 흘러가며 방해를 덜 받는 것입니다.
❓ Question in Lecture
Q1. 가장 높은 score를 선택하면 그만인데 왜 굳이 확률 분포에서 sampling을 하나요?
이 예제의 경우 가장 score가 높은 값만 사용하면 올바른 결과를 낼 수 없었습니다.
아까 'h' 다음 'e'를 출력한 것도 확률상 13% 낮은 비율이었기 때문입니다.
따라서 확률분포에서 sampling을 했기 때문에 'hello'를 만들 수 있었던 것입니다.
어떤 경우는 argmax probability(가장 높은 값을 취하는 방법)만 사용할 수 있습니다. 이게 더 안정적인 방법일 수 있습니다.
하지만 확률분포에서 sampling하는 방법을 사용하면 일반적으로 모델에서 다양성을 얻을 수 있습니다!
sampling 방법은 다양한 출력을 얻을 수 있다는 관점에서 좋은 방법이 될 수 있습니다.
Q2. Test time에 softmax vector을 one hot vector 대신에 넣어줄 수 있나요?
이럴 경우 두 가지 문제가 발생합니다.
- 입력이 Train time에서 본 입력과 달라집니다.
- 모델에게 Train time에서 보지 못한 입력 값을 주게 되면 대게는 모델이 아무 기능을 하지 못합니다.
- 실제로 vocabularies가 아주 크다는 것입니다.
- 예제에서는 vocab이 4개 밖에 없었습니다([h,e,l,o]).
그러나 한 step마다 단어(word)를 생성하는 모델이라고 보면 voca 안에는 이 세상의 모든 영어 단어가 들어가야 합니다.
voca는 수만 개 이상의 요소를 가지게 될 수 있습니다.
실제로는 one hot vector을 sparse vector operation으로 처리합니다.
만약 10,000 dimension을 가진 softmax vector가 들어오면 연산량이 어마어마 할 것입니다. 그래서 test time에서도 one hot을 사용합니다.
Q3.RNN이 Markov Assumption을 따르나요?
그렇지 않습니다. RNN은 이전 hidden state를 계속해서 앞으로 가져가기 때문입니다.
hidden state를 조건으로 마르코비아 가정을 하고 있다면, hidden state가 미래를 예언하는 시퀀스의 우리가 필요로 하는 모든 것이기 때문에. 시간을 통한 역전파를 시켜야 합니다.
Truncated Backprop은 very large sequence data의 gradient를 근사시키는 방법입니다.
Q4. 어떻게 다른 입력을 조절하는지? encoded image와 encoded question을 어떻게 조합할 수 있나요?
이렇게 요약된(encoded) 질문 벡터와 요약된 이미지를 어떻게 조합할 수 있는지에 대한 질문입니다.
가장 쉬운 방법은 하나의 concat으로 붙여서 FC-Layer의 입력으로 만드는 방법입니다.
Q5. 궁극적으로 W를 업데이트 해야 할텐데, W에 대한 그레디언트는 어떻게 되나요?
가중치 W에 대한 Local gradient는 해당 스텝에 해당하는 현재의 cell/hidden state로부터 전달됩니다. vanilla RNN의 경우 각 스텝의 가중치 행렬 W들이 서로 영향을 미쳤습니다.
반면 LSTM의 경우에는 가령 아주 긴 시퀀스가 있고 그레디언트가 맨 끝에서부터 전달되기 시작된다고 했을 때, 이 시퀀스의 backprop 과정에서 각 스텝마다 w에 대한 locla gradient가 있을 것입니다.
W의 local gradient는 cell/hidden state로부터 흘러옵니다. LSTM의 경우 cell state가 그레디언트를 잘 전달해주기 때문에 w에 대한 local gradient도 훨씬 더 깔끔하게 전달됩니다.
Q6. 여전히 Non-Linearities가 있으므로 (sigmoid) vanishing gradient 문제에 민감한가요?
그럴 지도 모릅니다. 가령 f의 경우 출력이 0~1이니 항상 1보다 작으므로 그레디어트가 점점 감소할 수 있습니다.
그래서 해결 방법으로 f의 biases를 양수로 초기화 시키는 방법이 있습니다. 이 방법을 이용해서 학습 초기에 forget gate의 값이 1에 가깝도록 해줍니다. 1에 가까운 값이기 때문에 적어도 학습 초기에는 그레디언트의 흐름이 비교적 원활합니다.
그리고 학습이 진행되면 f의 biases가 적절한 자기 자리를 찾아갑니다.
물론 LSTM에서도 vanishing gradient 문제가 발생할 수 있습니다. 하지만 vanilla RNN 보다 덜 민감한 이유는 매 스텝마다 f가 변하기 때문이고, 두 번째 이유는 LSTM에서는 Full Mat-mul이 아닌 element-wise multiplication을 수행하기 때문입니다.
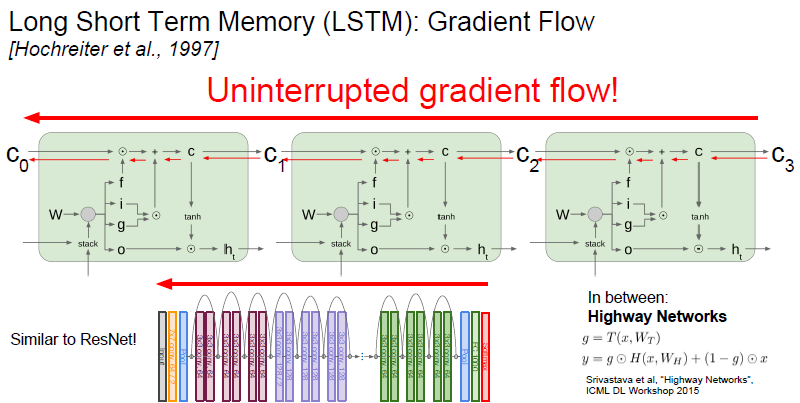
Resnet의 Backward pass에서 identity connection이 아주 유용했습니다. Identity mapping이 ResNet 그레디언트를 위한 고속도로 역할을 했습니다.
LSTM도 동일한 intuition입니다. LSTM의 Cell state의 element-wise mult가 그레디언트를 위한 고속도로 역할을 하기 때문입니다.
'버츄얼유튜버' 카테고리의 다른 글
| Visualizing and Understanding (0) | 2022.08.10 |
|---|---|
| Detection & Segmentation (0) | 2022.08.01 |
| 여러 CNN 아키텍처(LeNet, GoogleNet, Alexnet, VGG, ResNet) (0) | 2022.07.28 |
| Regularization (0) | 2022.07.27 |
| 메지로라이언이 시원시원하게 푸는 역전파&활성화, Optimizer (0) | 2022.07.21 |











